练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
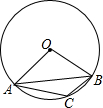
    19．如图，△ABC为⊙O的内接三角形，∠AOB=100°，则∠ACB的度数为（　　）
    A．100°B．130°C．150°D．160°

    分析 首先在优弧AB上取点D，连接AD，BD，然后由圆周角定理，求得∠D的度数，又由圆的内接四边形的性质，求得∠ACB的度数．

    解答 解：在优弧AB上取点D，连接AD，BD，
    ∵∠AOB=100°，
    ∴∠D=$\frac{1}{2}$∠AOB=50°，
    ∴∠ACB=180°-∠D=130°．
    故选B．

    点评 此题考查了圆周角定理以及圆的内接四边形的性质．注意准确作出辅助线是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．已知$\sqrt{2x+6}$和|y-$\sqrt{2}$|互为相反数，则x=-3，y=$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．计算：
    $\root{3}{-8}$=-2，
    分解因式：9x2-6x+1=（3x-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

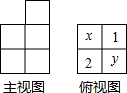    7．由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示，俯视图的方格中的字母和数字表示该位置上小立方体的个数，求x=1或2，y=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．（1）求x的值：9x2-4=0
    （2）计算：$|{-4}|+{（{\sqrt{2}+1}）^0}-\sqrt{12}$
    （3）已知：（x+5）3=-9，求x       
    （4）计算：$\sqrt{3{a^2}}÷\sqrt{\frac{a}{2}}×\frac{1}{2}\sqrt{\frac{2a}{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

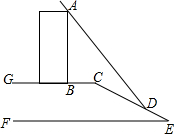    4．如图，某数学活动小组要测量楼AB的高度，楼AB在太阳光的照射下在水平面的影长BC为6米，在斜坡CE的影长CD为13米，身高1.5米的小红在水平面上的影长为1.35米，斜坡CE的坡度为1：2.4，求楼AB的高度．（坡度为铅直高度与水平宽度的比）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

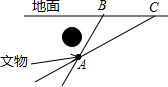    11．如图所示，某古代文物被探明埋于地下的A处，由于点A上方有一些管道，考古人员不能垂直向下挖掘，他们被允许从B处或C处挖掘，从B处挖掘时，最短路线BA与地面所成的锐角是56°，从C处挖掘时，最短路线CA与地面所成的锐角是30°，且BC=20m，若考古人员最终从B处挖掘，求挖掘的最短距离．（参考数据：sin56°=0.83，tan56°≈1.48，$\sqrt{3}$≈1.73，结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

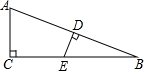    8．如图，Rt△ABC中，∠ACB=90°，AC=5，BC=12，AB的中垂线与BC交于点E，则BE的长等于（　　）
    A．$\frac{12}{5}$B．$\frac{13}{5}$C．$\frac{169}{24}$D．$\frac{60}{13}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，正方形ABCD的边长为3，AE=2BE，P是AC上一动点，则PB+PE的最小值为$\sqrt{13}$．

    查看答案和解析>>

    同步练习册答案