
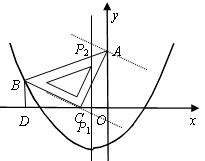
如图,在平面直角坐标系中,将一块等腰直角三角板ABC斜靠在两坐标轴上放在第二象限,点C的坐标为(-1,0).B点在抛物线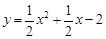 的图象上,过点B作
的图象上,过点B作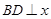 轴,垂足为D,且B点横坐标为
轴,垂足为D,且B点横坐标为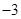 .
.
(1)求证: ;
;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使 △ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)先根据同角的余角相等证得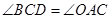 ,又
,又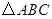 为等腰直角三角形,可得
为等腰直角三角形,可得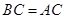 .即可证得结论;(2)
.即可证得结论;(2)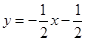 ;(3)
;(3)
解析试题分析:(1)先根据同角的余角相等证得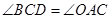 ,又
,又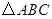 为等腰直角三角形,可得
为等腰直角三角形,可得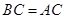 .即可证得结论;
.即可证得结论;
(2)由C点坐标可得BD=CO=1,即可得到B点坐标 设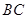 所在直线的函数关系式为
所在直线的函数关系式为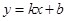 ,根据待定系数法即可求得结果;
,根据待定系数法即可求得结果;
(3)先求得抛物线的对称轴为直线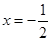 .再分以
.再分以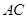 为直角边,点
为直角边,点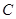 为直角顶点;以
为直角顶点;以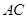 为直角边,点
为直角边,点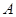 为直角顶点,两种情况根据一次函数的性质求解即可.
为直角顶点,两种情况根据一次函数的性质求解即可.
(1)∵ ,
,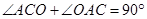 ,
,
∴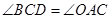 .
.
∵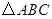 为等腰直角三角形,
为等腰直角三角形,
∴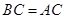 .
.
在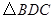 和
和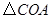 中
中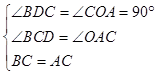
∴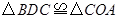 (AAS).
(AAS).
(2)∵C点坐标为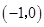 ,
,
∴BD=CO=1.
∵B点的横坐标为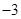 ,
,
∴B点坐标为 .
.
设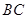 所在直线的函数关系式为
所在直线的函数关系式为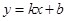 ,
,
则有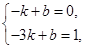 ,解得
,解得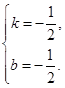
∴BC所在直线的函数关系式为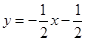 .
.
(3)存在. 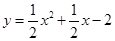 =
=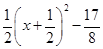 ,
,
∴对称轴为直线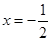 .
.
若以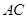 为直角边,点
为直角边,点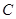 为直角顶点,对称轴上有一点
为直角顶点,对称轴上有一点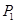 ,使
,使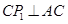 .
.
∵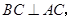
∴点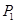 为直线
为直线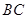 与对称轴直线
与对称轴直线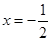 的交点.
的交点.
由题意得 ,解得
,解得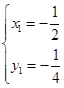
∴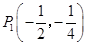 .
.
若以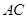 为直角边,点
为直角边,点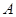 为直角顶点,对称轴上有一点
为直角顶点,对称轴上有一点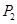 ,使
,使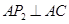 ,
,
过点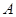 作
作 ,交对称轴直线
,交对称轴直线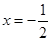 于点
于点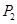 .
.
∵CD=OA,
∴A(0,2).
易求得直线 的解析式为
的解析式为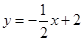 ,
,
由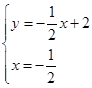 得
得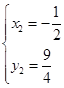 ,∴
,∴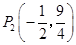 .
.
∴满足条件的点有两个,坐标分别为 .
.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
 如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.
如图,在平面直角坐标中,四边形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,点P为x轴上的一个动点,但是点P不与点0、点A重合.连接CP,D点是线段AB上一点,连接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是
(2012•渝北区一模)如图,在平面直角坐标xoy中,以坐标原点O为圆心,3为半径画圆,从此圆内(包括边界)的所有整数点(横、纵坐标均为整数)中任意选取一个点,其横、纵坐标之和为0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 ∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.
∠COA=45°,动点P从点O出发,在梯形OABC的边上运动,路径为O→A→B→C,到达点C时停止.作直线CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com