
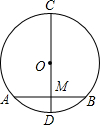
 如图,⊙O中,直径CD=10cm,弦AB⊥CD于点M,OM:MD=3:2,则AB的长是( )
如图,⊙O中,直径CD=10cm,弦AB⊥CD于点M,OM:MD=3:2,则AB的长是( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
分析 连接OA,由垂径定理得出AM=BM=$\frac{1}{2}$AB,由已知条件得出OA=OD=5cm,OM=3cm,由勾股定理求出AM,即可得出结果.
解答 解:连接OA,如图所示: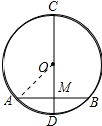
∵AB⊥CD,
∴∠OMA=90°,AM=BM=$\frac{1}{2}$AB,
∵CD=10cm,OM:MD=3:2,
∴OA=OD=5cm,OM=3cm,
∴AM=$\sqrt{O{A}^{2}-O{M}^{2}}$=$\sqrt{{5}^{2}{-3}^{2}}$=4(cm),
∴AB=2AM=8cm.
故选:D.
点评 本题考查了垂径定理、勾股定理;熟练掌握垂径定理,由勾股定理求出AM是解决问题的突破口.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.
如图,在平面直角坐标系中,四边形OABC是边长为8的正方形,M(8,m)、N(n,8)分别是线段AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
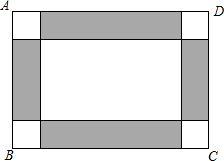 暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.
暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-2)2=1 | B. | (x-2)2=9 | C. | (x-4)2=21 | D. | (x-4)2=11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5-(-8)=-3 | B. | 6$\sqrt{5}$×$2\sqrt{5}$=12$\sqrt{5}$ | C. | $\frac{1}{4}$×(-4)=1 | D. | $\sqrt{\frac{1}{3}}$$÷\sqrt{\frac{1}{8}}$=$\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com