
分析 (1)根据有理数的乘法和减法进行计算即可;
(2)先对原式通分,再加减即可解答本题;
(3)先算乘除、再算加法即可解答本题;
(4)先将原式化简,再根据乘法的分配律进行计算即可.
解答 解:①1-$\frac{1}{3}$×(-3)2
=1-$\frac{1}{3}×9$
=1-3
=-2;
②-$\frac{1}{2}$+1$\frac{1}{5}$-2$\frac{7}{10}$
=$-\frac{1}{2}+\frac{6}{5}-\frac{27}{10}$
=$-\frac{5}{10}+\frac{12}{10}-\frac{27}{10}$
=-2;
③-2$\frac{1}{2}$+5$\frac{3}{5}$÷(-2)×(-$\frac{5}{14}$)
=$-\frac{5}{2}+\frac{28}{5}×(-\frac{1}{2})×(-\frac{5}{14})$
=$-\frac{5}{2}+1$
=-$\frac{3}{2}$;
④(-5)×(-3$\frac{2}{5}$)-(-7)×3$\frac{2}{5}$+12×(-3$\frac{2}{5}$)
=$5×\frac{17}{5}+7×\frac{17}{5}-12×\frac{17}{5}$
=$(5+7-12)×\frac{17}{5}$
=0×$\frac{17}{5}$
=0.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法,能用简便运算的用简便运算.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
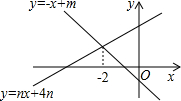 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( )
如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( )| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16cm | B. | 12cm | C. | 24cm | D. | 36cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC⊥AB,O为AC的中点,经过点O的直线交AD于E,交BC于F,连结AF、CE,现在添加一个适当的条件,使四边形AFCE是菱形,下列条件:①OE=OA;②EF⊥AC;③AF平分∠BAC;④E为AD中点.正确的有( )个.
如图,在?ABCD中,对角线AC⊥AB,O为AC的中点,经过点O的直线交AD于E,交BC于F,连结AF、CE,现在添加一个适当的条件,使四边形AFCE是菱形,下列条件:①OE=OA;②EF⊥AC;③AF平分∠BAC;④E为AD中点.正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
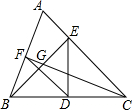 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )| A. | 67° | B. | 100° | C. | 113° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{3x}$ | C. | $\sqrt{2{x}^{3}}$ | D. | $\sqrt{\frac{5}{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com