
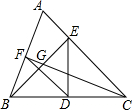
 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )| A. | 67° | B. | 100° | C. | 113° | D. | 120° |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.
如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5-(-8)=-3 | B. | 6$\sqrt{5}$×$2\sqrt{5}$=12$\sqrt{5}$ | C. | $\frac{1}{4}$×(-4)=1 | D. | $\sqrt{\frac{1}{3}}$$÷\sqrt{\frac{1}{8}}$=$\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
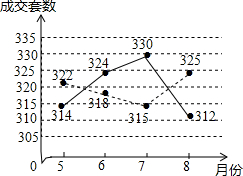 当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).
当今社会,住房问题是百姓较为关心的一个话题,某市的相关部门对该市汉江区和新洲区20135-8月的商品住房成交套数进行数据统计,并将汉江区和新洲区所统计的数据绘制车折线统计图(如图所示,图中实线表示的是汉江区的数据,虚线表示的是新洲区的数据).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com