
分析 作CD⊥AB于D,则∠ADC=∠BDC=90°,由三角形的面积求出CD,由勾股定理求出AD;分两种情况:①等腰△ABC为锐角三角形时,求出BD,由勾股定理求出BC即可;②等腰△ABC为钝角三角形时,求出BD,由勾股定理求出BC即可.
解答 解: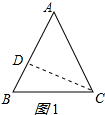 作CD⊥AB于D,
作CD⊥AB于D,
则∠ADC=∠BDC=90°,△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×5×CD=10,
解得:CD=4,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3;
分两种情况:
①等腰△ABC为锐角三角形时,如图1所示:
BD=AB-AD=2,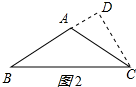
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$;
②等腰△ABC为钝角三角形时,如图2所示:
BD=AB+AD=8,
∴BD=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$;
综上所述:BC的长为2$\sqrt{5}$或4$\sqrt{5}$;
故答案为:2$\sqrt{5}$或4$\sqrt{5}$.
点评 本题考查了等腰三角形的性质、三角形的面积公式及勾股定理,解题的关键画出图形,分两种情况讨论.


科目:初中数学 来源: 题型:选择题
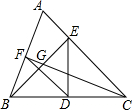 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )| A. | 67° | B. | 100° | C. | 113° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{3x}$ | C. | $\sqrt{2{x}^{3}}$ | D. | $\sqrt{\frac{5}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买方式 | 标价(元/条) | 优惠条件 |
| 实体店 | 40 | 全部按标价的8折出售 |
| 网店 | 40 | 购买100或100条以下,按标价出售; 购买100条以上,从101条开始按标价的7折出售(免邮寄费) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长.
如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com