
 如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长.
如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长. 分析 把相等的边靠在一起即可得到答案,有三种拼法.
解答 解:有三种拼法,如图1中,两条对角线都是m;
如图2中,对角线分别为n和$\sqrt{4{h}^{2}+{n}^{2}}$;
较长的对角线=2×$\sqrt{{h}^{2}+(\frac{n}{2})^{2}}$=$\sqrt{4{h}^{2}+{n}^{2}}$.
如图3中,对角线分别为h和$\sqrt{4{n}^{2}+{h}^{2}}$;
较长的对角线=2×$\sqrt{{n}^{2}+(\frac{h}{2})^{2}}$=$\sqrt{4{n}^{2}+{h}^{2}}$.
点评 本题考查平行四边形的判定、图形的平移旋转等知识,本题还考查了学生的动手能力、空间想象能力,解题的关键是相等的边靠在一起,且满足是平行四边形这个条件,属于中考常考题型.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
| A. | 该方程有两个相等的实数根 | |
| B. | 该方程有两个不相等的实数根,且它们互为相反数 | |
| C. | 该方程有一根为$\frac{{1+\sqrt{5}}}{2}$ | |
| D. | 该方程有一根恰为黄金比例 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
| 课桌 | -4 | -6 | -5 | +3 | -2 | +4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
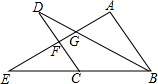 如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4.
如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com