
 如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$.
如图,在△ABE中∠AEB=90°,AB=$\sqrt{26}$,以AB为边在△ABE的同侧作正方形ABCD,点O为AC与BD的交点,连接OE,OE=2$\sqrt{2}$,点P为AB上一点,将△APE沿直线PE翻折得到△GPE,若PG⊥BE于点F,则BF=5-$\frac{5\sqrt{26}}{26}$. 分析 在BE上截取BM=AE,连接OM,OE,AC与BE交于点K,由△OAE≌△OBM得EO=OM,∠AOE=∠BOM,所以∠EOM=∠AOB=90°,得EM=$\sqrt{2}$OE,设AE=BM=a,在RT△ABE中,由AB2=AE2+BE2求出a,再证明AP=AE,利用$\frac{PB}{AB}=\frac{BF}{BE}$即可求出BF.
解答 解:如图,在BE上截取BM=AE,连接OM,OE,AC与BE交于点K,
∵四边形ABCD是正方形,
∴AC⊥BD,AO=OB,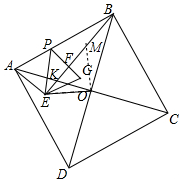
∴∠AEB=∠AOB=90°,
∴∠EAK+∠AKE=90°,∠BKO+∠OBM=90°,
∵∠BKO=∠AKE,
∴∠EAO=∠OBM,
在△OAE和△OBM中,
$\left\{\begin{array}{l}{OA=OB}\\{∠OAE=∠OBM}\\{AE=MB}\end{array}\right.$,
∴△OAE≌△OBM,
∴OE=OM,∠AOE=∠BOM,
∴∠EOM=∠AOB=90°,
∴EM=$\sqrt{2}$OE=4,设AE=BM=a,
在RT△ABE中,∵AB2=AE2+BE2,
∴26=a2+(a+4)2,
∵a>0,
∴a=1,
∵△PEG是由△PEA翻折,
∴PA=PG,∠APE=∠GPE,
∵PG⊥EB,AE⊥EB,
∴AE∥PG,
∴∠AEP=∠GPE=∠APE,
∴AP=AE=1,PB=$\sqrt{26}-1$,
∴$\frac{PB}{AB}=\frac{BF}{BE}$,
∴$\frac{\sqrt{26}-1}{\sqrt{26}}=\frac{BF}{5}$,
∴BF=5-$\frac{5\sqrt{26}}{26}$.
故答案为5-$\frac{5\sqrt{26}}{26}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质、翻折变换等知识,解题的关键是利用旋转的思想添加辅助线,构造全等三角形,属于中考填空题的压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )
在矩形ABCD中,BC=4,BG与对角线AC垂直且分别交AC,AD及射线CD于点E,F,G,当点F为AD中点时,∠ECF的正切值是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,…按照这种移动规律进行下去,第51次移动到点A51,那么点A51所表示的数为( )| A. | -74 | B. | -77 | C. | -80 | D. | -83 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.
如图,MN是半径为4cm的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
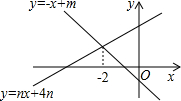 如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( )
如图,直线y=-x+m与y=nx+4n的交点的横坐标为-2,则关于x的不等式nx+4n>-x+m>0的整数解可能是( )| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
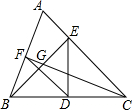 如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )
如图,在△ABC中,∠A=67°,D是BC的中点,BE⊥AC于点E,连接DE,点F在AB上,连接DF,恰有DF=DE,连接CF交BE于点G,则∠EGF的度数为( )| A. | 67° | B. | 100° | C. | 113° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com