
【题目】如图,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支架底端与桌面顶端的距离OA = 75厘米.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB =∠ACB = 37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37° ≈ 0.6,cos37°≈ 0.8,tan37° ≈ 0.75)


【答案】小桌板桌面的宽度BC约为37.5cm.
【解析】试题分析:延长CB交AO于点D.则CD⊥OA,在Rt△OBD中根据正弦函数求得BD,根据余弦函数求得OD,在Rt△ACD中,根据正切函数求得AD,然后根据AD+OD=OA=75,列出关于x的方程,解方程即可求得.
试题解析:延长CB交AO于点D.

∴CD⊥OA,
设BC=x,则OB=75-x,
在Rt△OBD中,OD=OBcos∠AOB,BD=OBsin∠AOB,
∴OD=(75-x)cos37°=0.8(75-x)=60-0.8x,
BD=(75-x)sin37°=0.6(75-x)=45-0.6x,
在Rt△ACD中,AD=DCtan∠ACB,
∴AD=(x+45-0.6x)tan37°=0.75(0.4x+45)=0.3x+33.75,
∵AD+OD=OA=75,
∴0.3x+33.75+60-0.8x=75,
解得x=37.5.
∴BC=37.5;
故小桌板桌面的宽度BC约为37.5cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在第一象限内作射线OC,与x轴的夹角为60°,在射线OC上取一点A,过点A作AH⊥x 轴于点H,在抛物线y=x2(x>0)上取一点P,在y轴上取一点Q,使得以P、O、Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知O是坐标原点,点A的坐标是(5,0),点B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和边OA上,将△BOE沿着OE对折,使点B落在OC上的F点处,将△ACH沿着CH对折,是点A落在OC上的G点处。
(1)求证:四边形OECH是平行四边形;
(2)如图2,当点B运动到使得点F,G重合时,判断四边形OECH的形状并说明理由;
(3)当点B运动到使得点F,G将对角线OC三等分时,求点B的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm, BC=26cm.,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动。规定其中一个动点到达端点时,另一个动点也随之停止运动。从运动开始,使PQ=CD,需要经过多长时间?
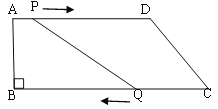
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程x2﹣x+a=0有实根.
(1)求a的取值范围;
(2)设x1、x2是方程的两个实数根,且满足(x1+1)(x2+1)=﹣1,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日孙老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5.
项目 | 第一次锻炼 | 第二次锻炼 | ||
步数(步) | 10000 | ① | ||
平均步长(米/步) | 0.6 | ② | ||
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)求孙老师第二次锻炼时平均步长减少的百分率;
(2)孙老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求孙老师这500米的平均步长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1)![]() 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
![]() 求
求![]() 的值;
的值;
![]() 若CD=2,求BP的长.
若CD=2,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市户籍人口1694000人,则该市户籍人口数据用科学记数法可表示为( )
A.1.694×104人
B.1.694×105人
C.1.694×106人
D.1.694×107人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
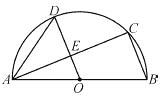
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com