
【题目】如图,已知点A1的坐标为(0,1),直线1为y=x.过点A1作A1B1⊥y轴交直线1于点B1,过点B1作A2B1⊥1交y轴于点A2;过点A2作A2B2⊥y轴交直线1于点B2,过点B2作A3B2⊥1交y轴于点A3,……,则AnBn的长是______.
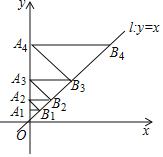
【答案】2n-1
【解析】
由点A1的坐标可得出点B1的坐标,进而可得出A1B1的长,由A2B1⊥1交y轴于点A2结合直线1为y=x可得出△A1A2B1为等腰直角三角形,根据等腰直角三角形的性质可得出点A2的坐标,利用一次函数图象上点的坐标可得出点B2的坐标,进而可得出A2B2的长,同理,可得出A3B3,A4B4,…的长,再根据各线段长度的变化可找出变化规律“AnBn=2n-1”,此题得解.
解:∵点A1的坐标为(0,1),
∴点B1的坐标为(1,1),A1B1=1.
∵A2B1⊥1交y轴于点A2,直线1为y=x,
∴△A1A2B1为等腰直角三角形,
∴点A2的坐标为(0,2),点B2的坐标为(2,2),
∴A2B2=2.
同理,可得:A3B3=4,A4B4=8,…,
∴AnBn=2n-1.
故答案为:2n-1.


科目:初中数学 来源: 题型:
【题目】如图1,边长为a的正方形发生形变后成为边长为a的菱形,如果这个菱形的一组对边之间的距离为h,我们把![]() 的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:
的值叫做这个菱形的“形变度”.例如,当形变后的菱形是如图2形状(被对角线BD分成2个等边三角形),则这个菱形的“形变度”为2:![]() .如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=
.如图3,正方形由16个边长为1的小正方形组成,形变后成为菱形,△AEF(A、E、F是格点)同时形变为△A′E′F′,若这个菱形的“形变度”k=![]() ,则S△A′E′F′=__
,则S△A′E′F′=__

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB经过圆心O,交⊙O于A、C两点,点D在⊙O上,∠A=∠B=30°.
(1)求证:BD是⊙O的切线;
(2)若点N在⊙O上,且DN⊥AB,垂足为M,NC=10,求AD的长.
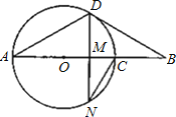
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市环保局决定购买A、B两种型号的扫地车共40辆,对城区所有公路地面进行清扫.已知1辆A型扫地车和2辆B型扫地车每周可以处理地面垃圾100吨,2辆A型扫地车和1辆B型扫地车每周可以处理垃圾110吨.
(1)求A、B两种型号的扫地车每辆每周分别可以处理垃圾多少吨?
(2)已知A型扫地车每辆价格为25万元,B型扫地车每辆价格为20万元,要想使环保局购买扫地车的资金不超过910万元,但每周处理垃圾的量又不低于1400吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少资金是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级社会实践小组去某商场调查商品的销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件,并以每件120元的价格销售了400件,商场准备采取促销措施,将剩下的衬衫降价销售.
(1)每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
(2)在(1)的条件下,某公司给员工发福利,在该商场促销钱购买了20件该品牌的衬衫发给员工,后因为有新员工加入,又要购买5件该衬衫,购买这5件衬衫时恰好赶上该商场进行促销活动,求该公司购买这25件衬衫的平均价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“数学小论文”评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为l:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有____篇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣2010)0+![]() ﹣2sin60°﹣3tan30°+
﹣2sin60°﹣3tan30°+![]() ;
;
(2)解方程:x2﹣6x+2=0;
(3)已知关于x的一元二次方程x2﹣mx﹣2=0.
①若﹣1是方程的一个根,求m的值和方程的另一根;
②证明:对于任意实数m,函数y=x2﹣mx﹣2的图象与x轴总有两个交点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com