练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于的一元二次方程．

    （1）求证：该方程有两个实数根；

    （2）若该方程的两个实数根、满足，求的值．

    【答案】（1）该方程有两个的实数根；（2）m=±4.

    【解析】试题分析：（1）求出△=b2﹣4ac的值，判定△≥0即可；

    （2）根据根与系数的关系可得x1+x2=4，再结合条件2x1+x2=2可得x1=﹣2，然后再把x的值代入方程可得4+8﹣m2+4=0，再解即可．

    试题解析：（1）证明：∵△=（﹣4）2﹣4×1×（﹣m2+4）=16+4m2﹣16=4m2≥0，∴该方程有两个实数根；

    （2）∵方程的两个实数根x1、x2，∴x1+x2=4．∵2x1+x2=2，∴x1+4=2，x1=﹣2，把x1=﹣2代入x2﹣4x﹣m2+4=0得：4+8﹣m2+4=0，m=±4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】右图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为轴、轴的正方向建立平面直角坐标系，有如下四个结论：

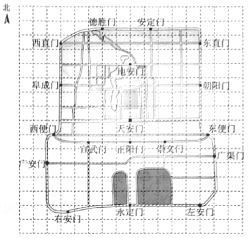
    ①当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（，）时，表示左安门的点的坐标为（5，）；

    ②当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（，）时，表示左安门的点的坐标为（10，）；

    ③当表示天安门的点的坐标为（1，1），表示广安门的点的坐标为（，）时，表示左安门的点的坐标为（，）；

    ④当表示天安门的点的坐标为（，），表示广安门的点的坐标为（，）时，表示左安门的点的坐标为（，）．

    上述结论中，所有正确结论的序号是

    A. ①②③ B. ②③④ C. ①④ D. ①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴上的点M，N表示的数分别是m，n，点M在表示0，1的两点（不包括这两点）之间移动，点N在表示-1，-2的两点（不包括这两点）之间移动，则下列判断正确的是（ ）

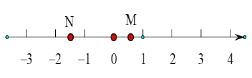
    A.的值一定小于0

    B.的值一定小于2

    C.的值可能比2000大

    D.的值不可能比2000大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

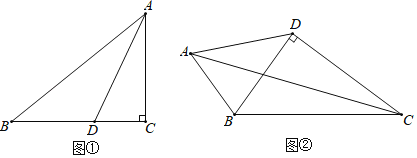
    【题目】如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”．

    （1）若△ABC是“准互余三角形”，∠C＞90°，∠A=60°，则∠B=　 　°；

    （2）如图①，在Rt△ABC中，∠ACB=90°，AC=4，BC=5．若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”．试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由．

    （3）如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，一次函数y=﹣x+4的图象与x轴和y轴分别相交于A、B两点．动点P从点A出发，在线段AO上以每秒3个单位长度的速度向点O作匀速运动，到达点O停止运动，点A关于点P的对称点为点Q，以线段PQ为边向上作正方形PQMN．设运动时间为t秒．

    （1）当t=秒时，点Q的坐标是　 　；

    （2）在运动过程中，设正方形PQMN与△AOB重叠部分的面积为S，求S与t的函数表达式；

    （3）若正方形PQMN对角线的交点为T，请直接写出在运动过程中OT+PT的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

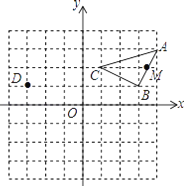
    【题目】阅读下面的文字，解答问题．

    如图，在平面直角坐标系中，点D的坐标是（﹣3，1），点A的坐标是（4，3）．

    （1）点B和点C的坐标分别是________、________．

    （2）将△ABC平移后使点C与点D重合，点A、B分别与点E、F重合，画出△DEF．并直接写出E点的坐标 ，F点的坐标 ．

    （3）若AB上的点M坐标为（x，y），则平移后的对应点M′的坐标为___　　_____．

    （4）求的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一副三角板中的两块直角三角板的直角顶点按如图方式叠放在一起，友情提示：，，.

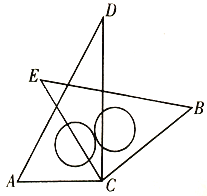
    （1）①若，则的度数为__________；

    ②若，则的度数为__________.

    （2）由（1）猜想与的数量关系，并说明理由；

    （3）当且点在直线的上方时，当这两块角尺有一组边互相平行时，请直接写出角度所有可能的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在矩形 ABCD 中，动点 E 从点 A 出发，沿 AB→BC 方向运动，当点 E 到达点 C 时 停止运动．过点 E 作 FE⊥AE，交 CD 于 F 点，设点 E 运动路程为 x，FC＝y，图②表示 y与 x 的函数关系的大致图像，则矩形 ABCD 的面积是（ ）

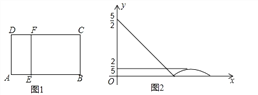
    A. B. 5 C. 6 D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，然后解答后面的问题．

    我们知道方程2x+3y=12有无数组解，但在实际生活中我们往往只需要求出其正整数解．例：由2x+3y=12，得，（x、y为正整数）∴则有0＜x＜6．又为正整数，则为正整数．

    由2与3互质，可知：x为3的倍数，从而x=3，代入．

    ∴2x+3y=12的正整数解为

    问题：

    （1）请你写出方程2x+y=5的一组正整数解：______；

    （2）若为自然数，则满足条件的x值有______个；

    A、2B、3C、4D、5

    （3）七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？

    查看答案和解析>>

    同步练习册答案