
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.
(1)当t=![]() 秒时,点Q的坐标是 ;
秒时,点Q的坐标是 ;
(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;
(3)若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.

【答案】(1)(4,0);(2)①当0<t≤1时,S =![]() t2;②当1<t≤
t2;②当1<t≤![]() 时,S =﹣
时,S =﹣![]() t2+18t;③当
t2+18t;③当![]() <t≤2时, S =﹣3t2+12;(3)OT+PT的最小值为
<t≤2时, S =﹣3t2+12;(3)OT+PT的最小值为![]() .
.
【解析】(1)先确定出点A的坐标,进而求出AP,利用对称性即可得出结论;
(2)分三种情况,①利用正方形的面积减去三角形的面积,②利用矩形的面积减去三角形的面积,③利用梯形的面积,即可得出结论;
(3)先确定出点T的运动轨迹,进而找出OT+PT最小时的点T的位置,即可得出结论.
(1)令y=0,
∴﹣![]() x+4=0,
x+4=0,
∴x=6,
∴A(6,0),
当t=![]() 秒时,AP=3×
秒时,AP=3×![]() =1,
=1,
∴OP=OA﹣AP=5,
∴P(5,0),
由对称性得,Q(4,0);
(2)当点Q在原点O时,OQ=6,
∴AP=![]() OQ=3,
OQ=3,
∴t=3÷3=1,
①当0<t≤1时,如图1,令x=0,
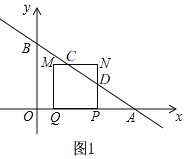
∴y=4,
∴B(0,4),
∴OB=4,
∵A(6,0),
∴OA=6,
在Rt△AOB中,tan∠OAB=![]() ,
,
由运动知,AP=3t,
∴P(6﹣3t,0),
∴Q(6﹣6t,0),
∴PQ=AP=3t,
∵四边形PQMN是正方形,
∴MN∥OA,PN=PQ=3t,
在Rt△APD中,tan∠OAB=![]() ,
,
∴PD=2t,
∴DN=t,
∵MN∥OA
∴∠DCN=∠OAB,
∴tan∠DCN=![]() ,
,
∴CN=![]() t,
t,
∴S=S正方形PQMN﹣S△CDN=(3t)2﹣![]() t×
t×![]() t=
t=![]() t2;
t2;
②当1<t≤![]() 时,如图2,同①的方法得,DN=t,CN=
时,如图2,同①的方法得,DN=t,CN=![]() t,
t,
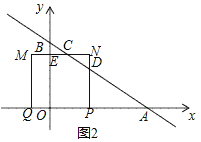
∴S=S矩形OENP﹣S△CDN=3t×(6﹣3t)﹣![]() t×
t×![]() t=﹣
t=﹣![]() t2+18t;
t2+18t;
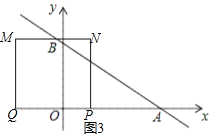
③当![]() <t≤2时,如图3,S=S梯形OBDP=
<t≤2时,如图3,S=S梯形OBDP=![]() (2t+4)(6﹣3t)=﹣3t2+12;
(2t+4)(6﹣3t)=﹣3t2+12;
(3)如图4,由运动知,P(6﹣3t,0),Q(6﹣6t,0),
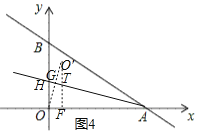
∴M(6﹣6t,3t),
∵T是正方形PQMN的对角线交点,
∴T(6﹣![]() t,
t,![]() t)
t)
∴点T是直线y=﹣![]() x+2上的一段线段,(﹣3≤x<6),
x+2上的一段线段,(﹣3≤x<6),
作出点O关于直线y=﹣![]() x+2的对称点O'交此直线于G,过点O'作O'F⊥x轴,则O'F就是OT+PT的最小值,
x+2的对称点O'交此直线于G,过点O'作O'F⊥x轴,则O'F就是OT+PT的最小值,
由对称知,OO'=2OG,
易知,OH=2,
∵OA=6,AH=![]() ,
,
∴S△AOH=![]() OH×OA=
OH×OA=![]() AH×OG,
AH×OG,
∴OG=![]() ,
,
∴OO'=![]()
在Rt△AOH中,sin∠OHA=![]() ,
,
∵∠HOG+∠AOG=90°,∠HOG+∠OHA=90°,
∴∠AOG=∠OHA,
在Rt△OFO'中,O'F=OO'sin∠O'OF=![]() ×
×![]() =
=![]() ,
,
即:OT+PT的最小值为![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
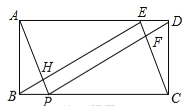
(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB经过点C(a,a),且交x轴于点A(m,0),交y轴于点B(0,n),且m,n满足![]() +(n﹣12)2=0.
+(n﹣12)2=0.
(1)求直线AB的解析式及C点坐标;
(2)过点C作CD⊥AB交x轴于点D,请在图1中画出图形,并求D点的坐标;
(3)如图2,点E(0,﹣2),点P为射线AB上一点,且∠CEP=45°,求点P的坐标.
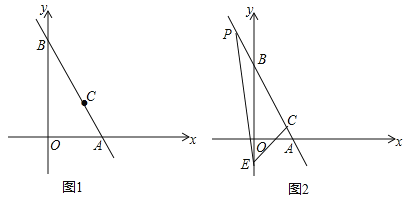
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式4x6y2- 3x2y- x- 7,次数是b,4a与b互为相反数,在数轴上,点A表示数a,点B表示数b.
(1)a=____________,b=____________
(2)若小蚂蚁甲从点A处以3个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以4单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点0处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.(写出解答过程)
(3)若小蚂蚁甲和乙约好分别从A,B两点,分别沿数轴甲向左,乙向右以相同的速度爬行,经过一段时间原路返回,刚好在16s时一起重新回到原出发点A和B,设小蚂蚁们出发t(s)时的速度为v(mm/s),v与t之间的关系如下图.(其中s表示时间单位秒,mm表示路程单位毫米)
t (s) | 0<t≤2 | 2<t≤5 | 5<t≤16 |
v(mm/s) | 10 | 16 | 8 |
①当2<t≤5时,你知道小蚂蚁甲与乙之间的距离吗?(用含有t的代数式表示);
②当t为__________________时,小蚂蚁甲乙之间的距离是42mm.(请直接写出答案)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() ,点E在线段AB上,
,点E在线段AB上,![]() ,点F在直线AD上,
,点F在直线AD上,![]() .
.
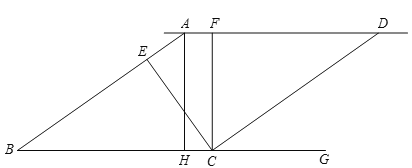
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 找出图中与
找出图中与![]() 相等的角,并说明理由;
相等的角,并说明理由;
![]() 在
在![]() 的条件下,点
的条件下,点![]() 不与点B、H重合
不与点B、H重合![]() 从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出
从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出![]() 的度数
的度数![]() 不必说明理由
不必说明理由![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
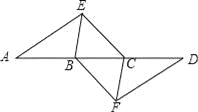
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是【 】
A.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则甲组数据比乙组数据大
,则甲组数据比乙组数据大
B.从1,2,3,4,5,中随机抽取一个数,是偶数的可能性比较大
C.数据3,5,4,1,﹣2的中位数是3
D.若某种游戏活动的中奖率是30%,则参加这种活动10次必有3次中奖
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com