
°æƒø°ø“—÷™∂ýœÓ Ω4x6y2- 3x2y- x- 7£¨¥Œ ˝ «b£¨4a”Îbª•Œ™œý∑¥ ˝£¨‘⁄ ˝÷·…œ£¨µ„A±Ì æ ˝a£¨µ„B±Ì æ ˝b£Æ
£®1£©a=____________£¨b=____________
£®2£©»Ù–°¬Ï“œº◊¥”µ„A¥¶“‘3∏ˆµ•Œª≥§∂»/√εƒÀŸ∂»œÚ◊Û‘À∂Ø£¨Õ¨ ±–°¬Ï“œ““¥”µ„B¥¶“‘4µ•Œª≥§∂»/√εƒÀŸ∂»“≤œÚ◊Û‘À∂Ø£¨±˚Õ¨—ßπ€≤Ï¡Ω÷ª–°¬Ï“œ‘À∂Ø£¨‘⁄À¸√«∏’ø™ º‘À∂Ø ±£¨‘⁄‘≠µ„0¥¶∑≈÷√“ªø≈∑π¡££¨““‘⁄≈ˆµΩ∑π¡£∫Û¡¢º¥±≥◊≈∑π¡£“‘‘≠¿¥µƒÀŸ∂»œÚœý∑¥µƒ∑ΩœÚ‘À∂Ø£¨…Ë‘À∂صƒ ±º‰Œ™t√Σ¨«Ûº◊°¢““¡Ω÷ª–°¬Ï“œµΩ‘≠µ„µƒæý¿Îœýµ» ±À˘∂‘”¶µƒ ±º‰t£Æ£®–¥≥ˆΩ‚¥π˝≥ã©
£®3£©»Ù–°¬Ï“œº◊∫Õ““‘º∫√∑÷±¥”A£¨B¡Ωµ„£¨∑÷±—ÿ ˝÷·º◊œÚ◊Û£¨““œÚ”““‘œýÕ¨µƒÀŸ∂»≈¿––£¨æ≠π˝“ª∂Œ ±º‰‘≠¬∑∑µªÿ£¨∏’∫√‘⁄16s ±“ª∆÷ÿ–¬ªÿµΩ‘≠≥ˆ∑¢µ„A∫ÕB£¨…Ë–°¬Ï“œ√«≥ˆ∑¢t£®s£© ±µƒÀŸ∂»Œ™v£®mm/s£©£¨v”Ît÷ƺ‰µƒπÿœµ»Áœ¬Õº£Æ£®∆‰÷–s±Ì æ ±º‰µ•Œª√Σ¨mm±Ì æ¬∑≥õ•Œª∫¡√◊£©
t £®s£© | 0<t°Ð2 | 2<t°Ð5 | 5<t°Ð16 |
v£®mm/s£© | 10 | 16 | 8 |
¢Ÿµ±2<t°Ð5 ±£¨ƒ„÷™µ¿–°¬Ï“œº◊”Γ“÷ƺ‰µƒæý¿Î¬£ø£®”√∫¨”–tµƒ¥˙ ˝ Ω±Ì æ£©£ª
¢⁄µ±tŒ™__________________ ±£¨–°¬Ï“œº◊““÷ƺ‰µƒæý¿Î «42mm£Æ£®«Î÷±Ω”–¥≥ˆ¥∞∏£©
![]()
°æ¥∞∏°ø£®1£©a=-2£¨b=8£ª£®2£©10ªÚ’þ![]() £ª£®3£©¢Ÿ32t-14£ª¢⁄1.6√ΪÚ14√Î.
£ª£®3£©¢Ÿ32t-14£ª¢⁄1.6√ΪÚ14√Î.
°æΩ‚Œˆ°ø
£®1£©∏˘æð∂ýœÓ Ωµƒ¥Œ ˝∂®“Âø…µ√b÷µ£¨‘Ÿ”…œý∑¥ ˝µƒ∂®“Âø…µ√a÷µ£ª
£®2£©∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫¢Ÿº◊°¢““¡Ω–°¬Ï“œæ˘œÚ◊Û‘À∂Ø£¨º¥0°Ðt°Ð2 ±£ª¢⁄º◊œÚ◊Û‘À∂Ø£¨““œÚ”“‘À∂Ø ±£¨º¥t£æ2 ±.∑÷±¡–∑Ω≥ëÛΩ‚º¥ø…£ª
£®3£©¢Ÿœ»º∆À„≥ˆ–°¬Ï“œº◊∫Õ““∏˜◊‘≈¿––µƒ◊Ь∑≥ã¨æð¥À≈–∂œµ±2<t°Ð5 ±£¨–°¬Ï“œº◊∫Õ““√ªªπ”–ø™ º∑µ≥Ã,¡– Ω«ÛΩ‚º¥ø…£ª
¢⁄œ»º∆À„≥ˆ–°¬Ï“œº◊∫Õ““ø™ º∑µ≥õƒ ±º‰Œ™µ⁄![]() √Î ±, »ª∫Û∑÷Àƒ÷÷«ÈøˆÃ÷¬€£∫µ±0<t°Ð2 ±£ªµ±2<t°Ð5 ±£ªµ±5<t°Ð
√Î ±, »ª∫Û∑÷Àƒ÷÷«ÈøˆÃ÷¬€£∫µ±0<t°Ð2 ±£ªµ±2<t°Ð5 ±£ªµ±5<t°Ð![]() ±£ªµ±
±£ªµ±![]() <t°Ð16 ±£Æ∑÷±¡–∑Ω≥ëÛΩ‚º¥ø….
<t°Ð16 ±£Æ∑÷±¡–∑Ω≥ëÛΩ‚º¥ø….
Ω‚£∫£®1£©°þ∂ýœÓ Ω4x6y2- 3x2y- x- 7¥Œ ˝ «8£¨
°ýb=8£¨
°þ4a”Îbª•Œ™œý∑¥ ˝£¨
°ý4a =-8£¨
°ýa =-2£¨
π ¥∞∏ «£∫-2£ª8.
£®2£©∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫
¢Ÿº◊°¢““¡Ω–°¬Ï“œæ˘œÚ◊Û‘À∂Ø£¨º¥0°Ðt°Ð2 ±£¨¥À ±OA=2+3t£¨OB=8-4t£¨
°þOA=OB£¨
°ý2+3t=8-4t
Ω‚µ√£¨t=![]() £ª
£ª
¢⁄º◊œÚ◊Û‘À∂Ø£¨““œÚ”“‘À∂Ø ±£¨º¥t£æ2 ±£¨
¥À ±OA=2+3t£¨OB=4t-8£¨
“¿Ã‚“‚µ√£¨2+3t=4t-8£¨
Ω‚µ√£¨t=10£Æ
¥£∫º◊°¢““¡Ω–°¬Ï“œµΩ‘≠µ„µƒæý¿Îœýµ» ±æ≠¿˙µƒ ±º‰ «![]() √ΪÚ10√ΣÆ
√ΪÚ10√ΣÆ
£®3£©¢Ÿ°þ–°¬Ï“œº◊∫Õ““Õ¨ ±≥ˆ∑¢“‘œýÕ¨µƒÀŸ∂»≈¿––£¨
°ý–°¬Ï“œº◊∫Õ““≈¿––µƒ¬∑≥à «œýÕ¨µƒ£¨∏˜◊‘≈¿––µƒ◊Ь∑≥Ã∂ºµ»”⁄
10°¡2+16°¡3+8°¡11=156£®mm£©£¨
°þ‘≠¬∑∑µªÿ£¨∏’∫√‘⁄16s ±“ª∆÷ÿ–¬ªÿµΩ‘≠≥ˆ∑¢µ„A∫ÕB£¨
°ý–°¬Ï“œº◊∫Õ““∑µ≥õƒ¬∑≥Ã∂ºµ»”⁄78mm,
°ýµ±2<t°Ð5 ±£¨–°¬Ï“œº◊∫Õ““√ªªπ”–ø™ º∑µ≥Ã,
°ýº◊”Γ“÷ƺ‰µƒæý¿Î=8-(-2)+ 10°¡2°¡2+16°¡(t-2) °¡2= 32t-14,
¢⁄…Ëa√Î «–°¬Ï“œº◊∫Õ““ø™ º∑µ≥Ã,”…£®3£©¢Ÿ÷™5<a°Ð16£¨
°ý10°¡2+16°¡3+8°¡£®a-5£©=78£¨
°ýa=![]() .
.
œ¬√Ê∑÷Àƒ÷÷«ÈøˆÃ÷¬€£∫
µ±0<t°Ð2 ±£¨–°¬Ï“œº◊∫Õ““√ªªπ”–ø™ º∑µ≥ã¨
8-(-2)+ 10°¡t°¡2= 42,
Ω‚µ√£¨t=1.6£ª
µ±2<t°Ð5 ±£¨–°¬Ï“œº◊∫Õ““√ªªπ”–ø™ º∑µ≥ã¨
32t-14=42,
Ω‚µ√£¨t=![]() <2£¨≤ª∫œÃ‚“‚£¨…·»•£ª
<2£¨≤ª∫œÃ‚“‚£¨…·»•£ª
µ±5<t°Ð![]() ±£¨–°¬Ï“œº◊∫Õ““√ªªπ”–ø™ º∑µ≥㨔…2<t°Ð5 ±µƒ«Èøˆø…÷™£¨¥À ±–°¬Ï“œº◊““÷ƺ‰µƒæý¿Î¥Û”⁄42mm£¨À˘“‘≤ª∫œÃ‚“‚£ª
±£¨–°¬Ï“œº◊∫Õ““√ªªπ”–ø™ º∑µ≥㨔…2<t°Ð5 ±µƒ«Èøˆø…÷™£¨¥À ±–°¬Ï“œº◊““÷ƺ‰µƒæý¿Î¥Û”⁄42mm£¨À˘“‘≤ª∫œÃ‚“‚£ª
µ±![]() <t°Ð16 ±£¨–°¬Ï“œº◊∫Õ““ø™ º∑µ≥ã¨
<t°Ð16 ±£¨–°¬Ï“œº◊∫Õ““ø™ º∑µ≥ã¨
8-(-2)+ 78°¡2-8°¡£®t-![]() £©°¡2= 42,
£©°¡2= 42,
Ω‚µ√£¨t=14£ª
◊€…œÀ˘ ˆ£¨µ±t=1.6√ΪÚ14√Î ±£¨–°¬Ï“œº◊““÷ƺ‰µƒæý¿Î «42mm£Æ
π ¥∞∏ «£∫1.6√ΪÚ14√Î.


 –°—ß—ßœ∞∫√∞Ô ÷œµ¡–¥∞∏
–°—ß—ßœ∞∫√∞Ô ÷œµ¡–¥∞∏ –°—ßÕ¨≤Ω»˝¡∑∫À–ƒ√ÐæÌœµ¡–¥∞∏
–°—ßÕ¨≤Ω»˝¡∑∫À–ƒ√ÐæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™«Ï◊£Ω®π˙∆þ Æ÷Ѓͣ¨ƒœ∏⁄«¯◊º±∏∂‘ƒ≥µ¿¬∑π§≥ÃΩ¯––∏ƒ‘Ï£¨»Ù«Îº◊π§≥Ã∂”µ•∂¿◊ˆ¥Àπ§≥ÖË4∏ˆ‘¬ÕÍ≥…£¨»Ù«Î““π§≥Ã∂”µ•∂¿◊ˆ¥Àπ§≥ÖË6∏ˆ‘¬ÕÍ≥…£¨»Ùº◊°¢““¡Ω∂”∫œ◊˜2∏ˆ‘¬∫Û£¨º◊π§≥Ã∂”µΩ∆⁄≥∑¿Î£¨‘Ú““π§≥Ã∂”‘Ÿµ•∂¿–˺∏∏ˆ‘¬ƒÐÕÍ≥…£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™![]() ”Î
”Î![]() ≥…’˝±»¿˝,«“
≥…’˝±»¿˝,«“![]() ±,
±,![]() .
.
(1)«Û![]() ”Î
”Î![]() µƒ∫Ø ˝πÿœµ Ω;
µƒ∫Ø ˝πÿœµ Ω;
(2)µ±![]() ±,«Û
±,«Û![]() µƒ÷µ;
µƒ÷µ;
(3)Ω´À˘µ√∫Ø ˝ÕºœÛ∆Ω“∆, πÀ¸π˝µ„(2, £≠1).«Û∆Ω“∆∫Û÷±œþµƒΩ‚Œˆ Ω.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨ ˝÷·…œµƒµ„M£¨N±Ì 浃 ˝∑÷± «m£¨n£¨µ„M‘⁄±Ì æ0£¨1µƒ¡Ωµ„£®≤ª∞¸¿®’‚¡Ωµ„£©÷ƺ‰“∆∂Ø£¨µ„N‘⁄±Ì æ-1£¨-2µƒ¡Ωµ„£®≤ª∞¸¿®’‚¡Ωµ„£©÷ƺ‰“∆∂Ø£¨‘Úœ¬¡–≈–∂œ’˝»∑µƒ «£® £©
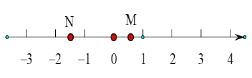
A.![]() µƒ÷µ“ª∂®–°”⁄0
µƒ÷µ“ª∂®–°”⁄0
B.![]() µƒ÷µ“ª∂®–°”⁄2
µƒ÷µ“ª∂®–°”⁄2
C.![]() µƒ÷µø…ƒÐ±»2000¥Û
µƒ÷µø…ƒÐ±»2000¥Û
D.![]() µƒ÷µ≤ªø…ƒÐ±»2000¥Û
µƒ÷µ≤ªø…ƒÐ±»2000¥Û
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÃΩæø”Î∑¢œ÷£∫»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œBAC=90°„£¨AB=AC£¨µ„D‘⁄µ◊±þBC…œ£¨AE=AD£¨¡¨Ω·DE.

£®1£©µ±°œBAD=60°„ ±£¨«Û°œCDEµƒ∂» ˝£ª
£®2£©µ±µ„D‘⁄BC £®µ„B°¢C≥˝Õ‚£© …œ‘À∂Ø ±£¨ ‘≤¬œÎ≤¢ÃΩæø°œBAD”ΰœCDEµƒ ˝¡øπÿœµ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
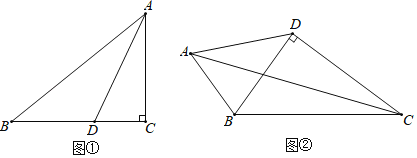
°æƒø°ø»Áπ˚»˝Ω«–Œµƒ¡Ω∏ˆƒ⁄Ω«¶¡”欬˙◊„2¶¡+¶¬=90°„£¨ƒ«√¥Œ“√«≥∆’‚—˘µƒ»˝Ω«–ŒŒ™°∞◊ºª•”ý»˝Ω«–Œ°±£Æ
£®1£©»Ù°˜ABC «°∞◊ºª•”ý»˝Ω«–Œ°±£¨°œC£æ90°„£¨°œA=60°„£¨‘Ú°œB=°° °°°„£ª
£®2£©»ÁÕº¢Ÿ£¨‘⁄Rt°˜ABC÷–£¨°œACB=90°„£¨AC=4£¨BC=5£Æ»ÙAD «°œBACµƒ∆Ω∑÷œþ£¨≤ªƒ—÷§√˜°˜ABD «°∞◊ºª•”ý»˝Ω«–Œ°±£Æ ‘Œ ‘⁄±þBC…œ «∑ҥʑ⁄µ„E£®“Ï”⁄µ„D£©£¨ πµ√°˜ABE“≤ «°∞◊ºª•”ý»˝Ω«–Œ°±£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆBEµƒ≥§£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©»ÁÕº¢⁄£¨‘⁄Àƒ±þ–ŒABCD÷–£¨AB=7£¨CD=12£¨BD°ÕCD£¨°œABD=2°œBCD£¨«“°˜ABC «°∞◊ºª•”ý»˝Ω«–Œ°±£¨«Û∂‘Ω«œþACµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“ª¥Œ∫Ø ˝y=©Å![]() x+4µƒÕºœÛ”Îx÷·∫Õy÷·∑÷±œýΩª”⁄A°¢B¡Ωµ„£Æ∂ص„P¥”µ„A≥ˆ∑¢£¨‘⁄œþ∂ŒAO…œ“‘√ø√Î3∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚµ„O◊˜‘»ÀŸ‘À∂Ø£¨µΩ¥Ôµ„OÕ£÷π‘À∂Ø£¨µ„Aπÿ”⁄µ„Pµƒ∂‘≥∆µ„Œ™µ„Q£¨“‘œþ∂ŒPQŒ™±þœÚ…œ◊˜’˝∑Ω–ŒPQMN£Æ…Ë‘À∂Ø ±º‰Œ™t√ΣÆ
x+4µƒÕºœÛ”Îx÷·∫Õy÷·∑÷±œýΩª”⁄A°¢B¡Ωµ„£Æ∂ص„P¥”µ„A≥ˆ∑¢£¨‘⁄œþ∂ŒAO…œ“‘√ø√Î3∏ˆµ•Œª≥§∂»µƒÀŸ∂»œÚµ„O◊˜‘»ÀŸ‘À∂Ø£¨µΩ¥Ôµ„OÕ£÷π‘À∂Ø£¨µ„Aπÿ”⁄µ„Pµƒ∂‘≥∆µ„Œ™µ„Q£¨“‘œþ∂ŒPQŒ™±þœÚ…œ◊˜’˝∑Ω–ŒPQMN£Æ…Ë‘À∂Ø ±º‰Œ™t√ΣÆ
£®1£©µ±t=![]() √Î ±£¨µ„Qµƒ◊¯±Í «°° °°£ª
√Î ±£¨µ„Qµƒ◊¯±Í «°° °°£ª
£®2£©‘⁄‘À∂Øπ˝≥Ã÷–£¨…Ë’˝∑Ω–ŒPQMN”ΰ˜AOB÷ÿµ˛≤ø∑÷µƒ√ʪ˝Œ™S£¨«ÛS”Îtµƒ∫Ø ˝±Ì¥Ô Ω£ª
£®3£©»Ù’˝∑Ω–ŒPQMN∂‘Ω«œþµƒΩªµ„Œ™T£¨«Î÷±Ω”–¥≥ˆ‘⁄‘À∂Øπ˝≥Ã÷–OT+PTµƒ◊Ó–°÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´“ª∏±»˝Ω«∞Â÷–µƒ¡ΩøÈ÷±Ω«»˝Ω«∞µƒ÷±Ω«∂•µ„![]() ∞¥»ÁÕº∑Ω Ωµ˛∑≈‘⁄“ª∆£¨”—«È÷ æ£∫
∞¥»ÁÕº∑Ω Ωµ˛∑≈‘⁄“ª∆£¨”—«È÷ æ£∫![]() £¨
£¨![]() £¨
£¨![]() .
.
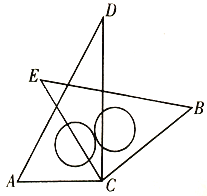
£®1£©¢Ÿ»Ù![]() £¨‘Ú
£¨‘Ú![]() µƒ∂» ˝Œ™__________£ª
µƒ∂» ˝Œ™__________£ª
¢⁄»Ù![]() £¨‘Ú
£¨‘Ú![]() µƒ∂» ˝Œ™__________.
µƒ∂» ˝Œ™__________.
£®2£©”…£®1£©≤¬œÎ![]() ”Î
”Î![]() µƒ ˝¡øπÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
µƒ ˝¡øπÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®3£©µ±![]() «“µ„
«“µ„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() µƒ…œ∑Ω ±£¨µ±’‚¡ΩøÈΩ«≥þ”–“ª◊ȱþª•œý∆Ω–– ±£¨«Î÷±Ω”–¥≥ˆ
µƒ…œ∑Ω ±£¨µ±’‚¡ΩøÈΩ«≥þ”–“ª◊ȱþª•œý∆Ω–– ±£¨«Î÷±Ω”–¥≥ˆ![]() Ω«∂»À˘”–ø…ƒÐµƒ÷µ.
Ω«∂»À˘”–ø…ƒÐµƒ÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº◊£¨““¡Ωº“∑˛◊∞…õ͜˙ €Õ¨“ª∆∑≈∆µƒŒ˜◊∞∫Õ¡Ï¥¯£¨Œ˜◊∞∂®º€∂º «√øÃ◊200‘™£¨¡Ï¥¯∂®º€∂º «√øÃı40‘™£Æœ÷¡Ωº“…õÍ∂º‘⁄¥Ÿœ˙£∫º◊µÍ£∫¬Ú“ªÃ◊Œ˜◊∞ÀÕ“ªÃı¡Ï¥¯£ª““µÍ£∫Œ˜◊∞∫Õ¡Ï¥¯∂º∞¥∂®º€µƒ90%∏∂øÓ£Æ
—ß–£∫œ≥™Õ≈“™π∫¬ÚŒ˜◊∞20Ã◊£¨¡Ï¥¯![]() Ãı£®
Ãı£®![]() £©£¨”…∫Û«⁄–ª¿œ ¶∏∫‘π∫¬Ú£¨«ÎŒ™–ª¿œ ¶≥ˆƒ±ªÆ≤þ£∫
£©£¨”…∫Û«⁄–ª¿œ ¶∏∫‘π∫¬Ú£¨«ÎŒ™–ª¿œ ¶≥ˆƒ±ªÆ≤þ£∫
£®1£©»Ù÷ª‘⁄“ªº“…õÍπ∫¬Ú£¨µ±![]() ±£¨–ª¿œ ¶—°‘Òƒƒº“…õÍπ∫¬ÚŒ˜◊∞∫Õ¡Ï¥¯∏¸ªÆÀ„£ø
±£¨–ª¿œ ¶—°‘Òƒƒº“…õÍπ∫¬ÚŒ˜◊∞∫Õ¡Ï¥¯∏¸ªÆÀ„£ø
£®2£©»Ù÷ª‘⁄“ªº“…õÍπ∫¬Ú£¨«Î”√∫¨![]() µƒ¥˙ ˝ Ω∑÷±±Ì æ‘⁄¡Ωº“…õ͵ƒª®∑—£ª
µƒ¥˙ ˝ Ω∑÷±±Ì æ‘⁄¡Ωº“…õ͵ƒª®∑—£ª
£®3£©µ±![]() ±£¨«Î…˺∆◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏≤¢«Û≥ˆ◊Ó…Ÿµƒª®∑— «∂ý…Ÿ£Æ
±£¨«Î…˺∆◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏≤¢«Û≥ˆ◊Ó…Ÿµƒª®∑— «∂ý…Ÿ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com