
【题目】甲,乙两家服装商店销售同一品牌的西装和领带,西装定价都是每套200元,领带定价都是每条40元.现两家商店都在促销:甲店:买一套西装送一条领带;乙店:西装和领带都按定价的90%付款.
学校合唱团要购买西装20套,领带![]() 条(
条(![]() ),由后勤谢老师负责购买,请为谢老师出谋划策:
),由后勤谢老师负责购买,请为谢老师出谋划策:
(1)若只在一家商店购买,当![]() 时,谢老师选择哪家商店购买西装和领带更划算?
时,谢老师选择哪家商店购买西装和领带更划算?
(2)若只在一家商店购买,请用含![]() 的代数式分别表示在两家商店的花费;
的代数式分别表示在两家商店的花费;
(3)当![]() 时,请设计最省钱的购买方案并求出最少的花费是多少.
时,请设计最省钱的购买方案并求出最少的花费是多少.
【答案】(1)若只在一家商店购买,当![]() 时,谢老师选择甲商店购买西装和领带更划算.
时,谢老师选择甲商店购买西装和领带更划算.
(2)若只在一家商店购买,在甲商店的花费为![]() 元,在乙商店的花费为
元,在乙商店的花费为![]() 元.
元.
(3)当![]() 时,最省钱的购买方案为在甲商店购买20套西装,20条领带,在乙商店购买0套西装,40条领带,最少的花费是5440元.
时,最省钱的购买方案为在甲商店购买20套西装,20条领带,在乙商店购买0套西装,40条领带,最少的花费是5440元.
【解析】
(1)分别根据题意计算出若只在甲购买和若只在乙购买的花费,比较两个花费的大小,即可判断哪种方案更划算.
(2)根据题意列出代数式表示即可.
(3)设在甲商店购买x套西装,x条领带,即在乙商店购买![]() 套西装,
套西装,![]() 条领带,总花费为y元,可得方程
条领带,总花费为y元,可得方程![]() ,再根据
,再根据![]() ,即可确定最省钱的购买方案.
,即可确定最省钱的购买方案.
(1)若只在甲购买:![]() (元)
(元)
若只在乙购买:![]() (元)
(元)
∵![]()
若只在一家商店购买,当![]() 时,谢老师选择甲商店购买西装和领带更划算.
时,谢老师选择甲商店购买西装和领带更划算.
(2)若只在甲购买: ![]()
若只在乙购买: ![]()
故若只在一家商店购买,在甲商店的花费为![]() 元,在乙商店的花费为
元,在乙商店的花费为![]() 元.
元.
(3)∵单买领带时,乙商店比甲商店便宜
∴要想花费最少,在甲商店购买的西装套数等于领带的条数
∴设在甲商店购买x套西装,x条领带,即在乙商店购买![]() 套西装,
套西装,![]() 条领带,总花费为y元
条领带,总花费为y元
![]()
![]() .
.
∵![]()
∴当![]() 时,总花费y有最小值
时,总花费y有最小值
最小值为![]()
故当![]() 时,最省钱的购买方案为在甲商店购买20套西装,20条领带,在乙商店购买0套西装,40条领带,最少的花费是5440元.
时,最省钱的购买方案为在甲商店购买20套西装,20条领带,在乙商店购买0套西装,40条领带,最少的花费是5440元.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】已知多项式4x6y2- 3x2y- x- 7,次数是b,4a与b互为相反数,在数轴上,点A表示数a,点B表示数b.
(1)a=____________,b=____________
(2)若小蚂蚁甲从点A处以3个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以4单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点0处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.(写出解答过程)
(3)若小蚂蚁甲和乙约好分别从A,B两点,分别沿数轴甲向左,乙向右以相同的速度爬行,经过一段时间原路返回,刚好在16s时一起重新回到原出发点A和B,设小蚂蚁们出发t(s)时的速度为v(mm/s),v与t之间的关系如下图.(其中s表示时间单位秒,mm表示路程单位毫米)
t (s) | 0<t≤2 | 2<t≤5 | 5<t≤16 |
v(mm/s) | 10 | 16 | 8 |
①当2<t≤5时,你知道小蚂蚁甲与乙之间的距离吗?(用含有t的代数式表示);
②当t为__________________时,小蚂蚁甲乙之间的距离是42mm.(请直接写出答案)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
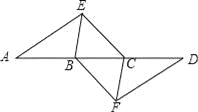
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED 灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了 LED 灯泡与普通白炽灯泡共 300 个,LED 灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利 3 200 元,求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120 个, 在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的 30%, 并求出此时这批灯泡的总利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人驾车从![]() 地出发在一条笔直的南北方向上来回行驶,向北行驶为正,向南行驶为负,行驶的路程情况如下(单位:千米):
地出发在一条笔直的南北方向上来回行驶,向北行驶为正,向南行驶为负,行驶的路程情况如下(单位:千米):![]() .
.
![]() 该人在完成上述
该人在完成上述![]() 次行车后在
次行车后在![]() 地的哪一侧?距
地的哪一侧?距![]() 地多少千米?
地多少千米?
![]() 如果这辆车每行驶
如果这辆车每行驶![]() 千米的耗油量为
千米的耗油量为![]() 升,这一天共耗油多少升?
升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永祚寺双塔,又名凌霄双塔,是山西省会太原现存古建筑中最高的建筑,位于太原市城区东南向山脚畔.数学活动小组的同学对其中一个塔进行了测量.测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为48 m,塔的顶端为点A,且AB⊥CB,在点E处竖直放一根标杆,其顶端为D,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得CE=2 m.
(1)方法1,已知标杆DE=2.2 m,求该塔的高度;
(2)方法2,测量得∠ACB=47.5°,已知tan47.5°≈1.09,求该塔的高度;
(3)假如该塔的高度在方法1和方法2测得的结果之间,你认为该塔的高度大约是多少米?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是【 】
A.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则甲组数据比乙组数据大
,则甲组数据比乙组数据大
B.从1,2,3,4,5,中随机抽取一个数,是偶数的可能性比较大
C.数据3,5,4,1,﹣2的中位数是3
D.若某种游戏活动的中奖率是30%,则参加这种活动10次必有3次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在五月份准备组织部分员工到背景旅游7天,现联系了甲、乙两家旅行社,两家旅行社报价均为每人7天共2000天,两家旅行社同时都对10人以上的团体推出了优惠举措;甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位员工的费用,其余员工八折优惠.
(1)如果设参加旅游的员工共有![]() 人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含
人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含![]() 的式子表示,并化简)
的式子表示,并化简)
(2)假如这个单位有20名员工参加旅游,该单位选择哪一家旅行社比较合算?并说明理由.
(3)假如这7天的日期之和为63的倍数,则他们可能于五月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在坐标平面内,点O是坐标原点,A(0,6)、B(2![]() ,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应。
,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应。
(1)求点C的坐标;
(2)动点F从点O出发,以2个单位长度/秒的速度沿折线O—A—C向终点C运动,设△FOB的面积为S(S≠0),点F的运动时间为t秒,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,过点B作x轴垂线,交AC于点E,在点F的运动过程中,当t为何值时,△BEF是以BE为腰的等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com