
【题目】同学们知道数学中的整体思想吗?在解决某些问题时,常常需要运用整体的方式对问题进行处理,如:整体思考、整体变形、把一个式子看作整体等,这样可以使问题简化并迅速求解.试运用整体的数学思想方法解决下列问题:
(1)把下列各式分解因式:
①![]() ②
②![]()
(2)①已知![]() 则
则![]() 的值为 .
的值为 .
②已知![]() 那么
那么![]() .
.
③已知![]() 求
求![]() 的值.
的值.
 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ﹙
﹙![]() ,
,![]() ﹚,
﹚,![]() ﹙
﹙![]() ,
,![]() ﹚,交
﹚,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.

![]() 求反比例函数
求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
![]() 连接
连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
![]() 根据图象写出使一次函数的值小于反比例函数的值的
根据图象写出使一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )
,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )

A. ①②③④ B. ②③④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过点
的图象过点![]() 和点
和点![]() ,对称轴为直线
,对称轴为直线![]() .
.

![]() 求该二次函数的关系式和顶点坐标;
求该二次函数的关系式和顶点坐标;
![]() 结合图象,解答下列问题:
结合图象,解答下列问题:
①当![]() 时,求函数
时,求函数![]() 的取值范围.
的取值范围.
②当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E在CD边上,将△ADE沿AE对折得到△AFE,延长EF交BC边于点G,连结AG.给出结论:①△ABG≌△AFG;②∠EAG=45°;③∠AGB+∠AED=135°.其中正确的结论有( )

A.只有①B.①②C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
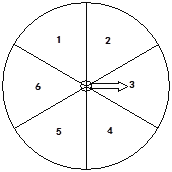
其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥NN于点M,BN⊥MN于N.
(1)求证:△AMC≌△CNB;
(2)求证:MN=AM+BN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬天,小芳给自己家刚刚装满水且显示温度为![]() 的太阳能热水器里的水加热.她每过一段时间去观察一下显示温度,并记录如下:
的太阳能热水器里的水加热.她每过一段时间去观察一下显示温度,并记录如下:
时间(分钟) | 0 | 5 | 10 | 15 | 20 | …… |
显示温度( | 16 | 17 | 18 | 19 | 20 | …… |
(1)请直接写出显示温度(![]() )与加热时间(
)与加热时间(![]() )之间的函数关系式;
)之间的函数关系式;
(2)如果她给热水器设定的最高温度为![]() ,问:要加热多长时间才能达到设定的最高温度?
,问:要加热多长时间才能达到设定的最高温度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面图形,解答问题:

(1)在△ABC中,AB=AC,∠BAC=100°,DE、FG分别是边AB、AC的垂直平分线(如图1),求∠DAG的度数?
(2)在(1)中,若去掉“AB=AC”的条件,其余条件不变(如图2),还能求出∠DAG的度数吗?若能,请求出∠DAG的度数;若不能,请说明理由;
(3)在(图2)的情况下试探索△ADG的周长与BC长的关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com