
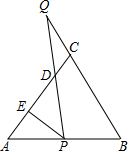
 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,则:①PD=DQ;②∠Q=30°;③DE=$\frac{1}{2}$AC;④AE=$\frac{1}{2}$CQ.其中正确的结论是①③④.(把所有正确结论的序号都写在横线上).
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,则:①PD=DQ;②∠Q=30°;③DE=$\frac{1}{2}$AC;④AE=$\frac{1}{2}$CQ.其中正确的结论是①③④.(把所有正确结论的序号都写在横线上). 分析 ①作辅助线,证明△PFD≌△QCD,可以得:PD=DQ;
②由全等可知:∠DPF=∠Q,由QP与AB不垂直,可以得∠Q不一定为30°;
③根据等腰三角线三线合一得:EF=$\frac{1}{2}$AF,由全等得:DF=$\frac{1}{2}$FC,两式相加可得结论;
④根据30°角所对的直角边是斜边一半可得结论.
解答 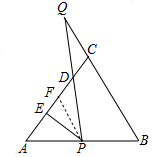 解:①过P作PF∥BQ,交AC于F,
解:①过P作PF∥BQ,交AC于F,
∵△ABC是等边三角形,
∴∠ACB=∠A=60°,
∵PF∥BQ,
∴∠AFP=∠ACB=60°,∠PFD=∠QCD,
∴△AFP是等边三角形,
∴PF=PA,
∵PA=CQ,
∴PF=CQ,
在△PFD和△QCD中,
∵$\left\{\begin{array}{l}{∠ADP=∠CDQ}\\{∠PFD=∠QCD}\\{PF=CQ}\end{array}\right.$,
∴△PFD≌△QCD(AAS),
∴PD=DQ;
所以①结论正确;
②由①得:△PFD≌△QCD,
∴∠DPF=∠Q,
∵△APF等边三角形,
∴∠APF=60°,
∵QP与AB不一定垂直,
∴∠Q不一定为30°,
所以②结论不正确;
③∵△APF是等边三角形,PE⊥AC,
∴EF=$\frac{1}{2}$AF,
∵△PFD≌△QCD,
∴DF=DC,
∴DF=$\frac{1}{2}$FC,
∴DE=EF+DF=$\frac{1}{2}$AF+$\frac{1}{2}$FC=$\frac{1}{2}$AC,
所以③结论正确;
④在Rt△AEP中,∠A=60°,
∴∠APE=30°,
∴AE=$\frac{1}{2}$AP,
∴AE=$\frac{1}{2}$CQ,
所以④结论正确;
所以本题结论正确的有:①③④;
故答案为:①③④.
点评 本题考查了等边三角形的性质和判定、三角形全等的性质和判定、直角三角形30°角的性质,作辅助线构建全等三角形是本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
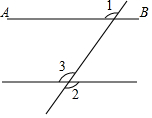 已知,如图,∠1=120°,∠2=120°,求证:AB∥CD.
已知,如图,∠1=120°,∠2=120°,求证:AB∥CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com