
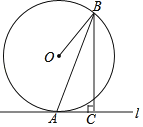
【题目】如图,已知直线l切⊙O于点A,B为⊙O上一点,过点B作BC⊥l,垂足为点C,连接AB、OB.
(1)求证:∠ABC=∠ABO;
(2)若AB=![]() ,AC=1,求⊙O的半径.
,AC=1,求⊙O的半径.
【答案】(1)详见解析;(2)⊙O的半径是![]() .
.
【解析】
(1)连接OA,求出OA∥BC,根据平行线的性质和等腰三角形的性质得出∠OBA=∠OAB,∠OBA=∠ABC,即可得出答案;
(2)根据矩形的性质求出OD=AC=1,根据勾股定理求出BC,根据垂径定理求出BD,再根据勾股定理求出OB即可.
(1)证明:连接OA,
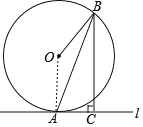
∵OB=OA,
∴∠OBA=∠OAB,
∵AC切⊙O于A,
∴OA⊥AC,
∵BC⊥AC,
∴OA∥BC,
∴∠OBA=∠ABC,
∴∠ABC=∠ABO;
(2)解:过O作OD⊥BC于D,
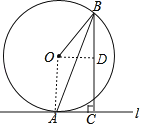
∵OD⊥BC,BC⊥AC,OA⊥AC,
∴∠ODC=∠DCA=∠OAC=90°,
∴OD=AC=1,
在Rt△ACB中,AB=![]() ,AC=1,由勾股定理得:BC=
,AC=1,由勾股定理得:BC=![]() =3,
=3,
∵OD⊥BC,OD过O,
∴BD=DC=![]() BC=
BC=![]() =1.5,
=1.5,
在Rt△ODB中,由勾股定理得:OB=![]() ,
,
即⊙O的半径是![]() .
.


科目:初中数学 来源: 题型:
【题目】有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
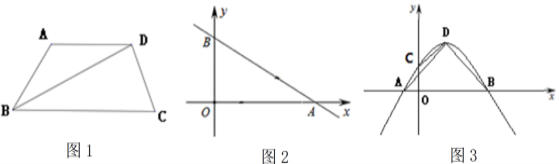
(1)如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;
(2)如图2,直线![]() 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;
(3)如图3,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),与y轴交于点
轴交于A、B两点(点A在点B的左侧),与y轴交于点![]() ,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①
,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:①![]() ;②顶点D在以AB为直径的圆上. 点
;②顶点D在以AB为直径的圆上. 点![]() 是抛物线
是抛物线![]() 上任意一点,且
上任意一点,且![]() .若
.若![]() 恒成立,求m的最小值.
恒成立,求m的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
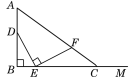
【题目】如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=![]() DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式为( )
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-
D.-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为﹣3和1;④当x<1时,y<0.其中正确的命题是( )
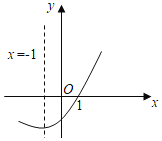
A.②③B.①③C.①②D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为5,D、E分别是边AB、AC上的点,将△ADE沿DE折叠,点A恰好落在BC边上的点F处,若BF=2,则BD的长是( )
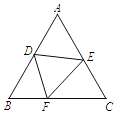
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
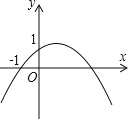
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
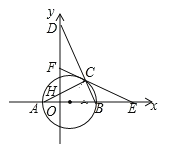
【题目】如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(﹣1,0)、C(3,2![]() ),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
(1)求⊙P的半径;
(2)当∠A=∠DCF时,求证:CE是⊙P的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC,OC=2,抛物线y=ax2+c过A,B,C三点,D为抛物线上一点,连接BD且tan∠DBC=![]() .
.

(1)求直线BD和抛物线所表示的函数解析式.
(2)如果在抛物线上有一点E,使得S△EBC=S△ABD,求这时E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一课外活动小组为了了解学生最喜欢的球类运动况,随机抽查了本校九年级的200名学生,调查的结果如图所示,请根据该扇形统计图解答以下问题:
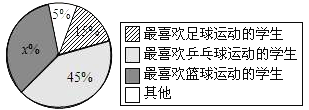
(1)图中![]() 的值是________;
的值是________;
(2)被查的200名生中最喜欢球运动的学生有________人;
(3)若由3名最喜欢篮球运动的学生(记为![]() ),1名最喜欢乒乓球运动的学生(记为
),1名最喜欢乒乓球运动的学生(记为![]() ),1名最喜欢足球运动的学生(记为
),1名最喜欢足球运动的学生(记为![]() )组队外出参加一次联谊活动.欲从中选出2人担任组长(不分正副),列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率.
)组队外出参加一次联谊活动.欲从中选出2人担任组长(不分正副),列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com