
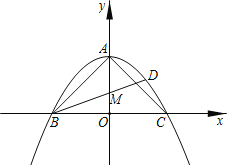
【题目】如图,等腰直角△ABC,OC=2,抛物线y=ax2+c过A,B,C三点,D为抛物线上一点,连接BD且tan∠DBC=![]() .
.

(1)求直线BD和抛物线所表示的函数解析式.
(2)如果在抛物线上有一点E,使得S△EBC=S△ABD,求这时E点坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或 或
或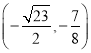
【解析】
(1)根据题意得到A(0,2),B(2,0),C(2,0),根据待定系数法即可求得抛物线的解析式,设BD与y轴的交点为M,由tan∠DBC=![]() ,求得M的坐标为(0,1),根据待定系数法即可求得直线BD的解析式;
,求得M的坐标为(0,1),根据待定系数法即可求得直线BD的解析式;
(2)解析式联立求得D的坐标,然后根据S△ABD=S△ABM+S△ADM求得△EBC面积,根据面积公式求得E的纵坐标,把纵坐标代入抛物线解析式即可求得横坐标,得到E的坐标.
(1)等腰直角△ABC,OC=2,
∴OA=OB=OC=2,
∴A(0,2),B(﹣2,0),C(2,0),
∵抛物线y=ax2+c过A,B,C三点,
∴![]() ,解得
,解得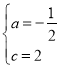 ,
,
∴抛物线的解析式为y=﹣![]() +2;
+2;
∵tan∠DBC=![]() ,
,
设BD与y轴的交点为M,
∴![]() =
=![]() ,
,
∴OM=2×![]() =1,
=1,
∴M(0,1),
设直线BD的解析式为y=kx+b,
把B(﹣2,0),M(0,1)代入得![]() ,
,
解得![]() ,
,
∴直线BD的解析式为y=![]() +1;
+1;
(2)解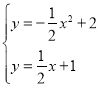 得
得![]() 或
或![]() ,
,
∴D(1,![]() ),
),
∴S△ABD=S△ABM+S△ADM=![]() ×(2﹣1)×2+
×(2﹣1)×2+![]() (2﹣1)×
(2﹣1)×![]() =
=![]() ,
,
∵S△EBC=S△ABD,
∴![]() BC|yE|=
BC|yE|=![]() ,即
,即![]() |yE|=
|yE|=![]() ,
,
∴|yE|=![]() ,
,
∴E的纵坐标为±![]() ,
,
把y=![]() 代入y=﹣
代入y=﹣![]() +2得,
+2得,![]() =﹣
=﹣![]() +2,
+2,
解得x=±![]() ,
,
把y=﹣![]() 代入y=﹣
代入y=﹣![]() +2得,﹣
+2得,﹣![]() =﹣
=﹣![]() +2,
+2,
解得x=±![]() ,
,
∴E点的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
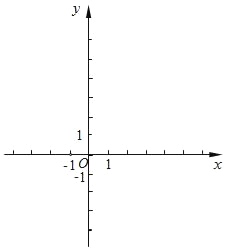
【题目】在平面直角坐标系xOy(如图)中,抛物线y=ax2+bx+2经过点A(4,0)、B(2,2),与y轴的交点为C.
(1)试求这个抛物线的表达式;
(2)如果这个抛物线的顶点为M,求△AMC的面积;
(3)如果这个抛物线的对称轴与直线BC交于点D,点E在线段AB上,且∠DOE=45°,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
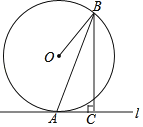
【题目】如图,已知直线l切⊙O于点A,B为⊙O上一点,过点B作BC⊥l,垂足为点C,连接AB、OB.
(1)求证:∠ABC=∠ABO;
(2)若AB=![]() ,AC=1,求⊙O的半径.
,AC=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=![]() 有 个实数根;
有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
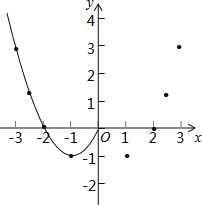
查看答案和解析>>
科目:初中数学 来源: 题型:
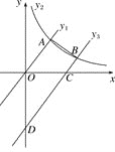
【题目】如图,直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (x>0)交于点A,将直线y1=
(x>0)交于点A,将直线y1=![]() x向下平移4个单位后称该直线为y3,若y3与双曲线交于B,与x轴交于C,与y轴交于D,AO=2BC,连接AB,则以下结论错误的有( )
x向下平移4个单位后称该直线为y3,若y3与双曲线交于B,与x轴交于C,与y轴交于D,AO=2BC,连接AB,则以下结论错误的有( )
①点C坐标为(3,0);②k=![]() ;③S四边形OCBA=
;③S四边形OCBA=![]() ;④当2<x<4时,有y1>y2>y3;⑤S四边形ABDO=2S△COD.
;④当2<x<4时,有y1>y2>y3;⑤S四边形ABDO=2S△COD.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
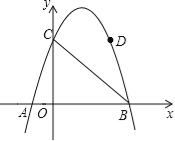
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.
(1)求tan∠DBC的值;
(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
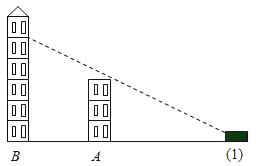
【题目】小明开着汽车在平坦的公路上行驶,前放出现两座建筑物A、B(如图),在(1)处小颖能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
(1)请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.
(2)若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
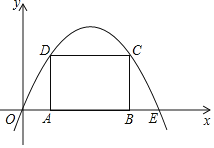
【题目】如图,抛物线y=ax2+bx(a<0)过点E(10,0),矩形ABCD的边AB在线段OE上(点A在点B的左边),点C,D在抛物线上.设A(t,0),当t=2时,AD=4.
(1)求抛物线的函数表达式.
(2)当t为何值时,矩形ABCD的周长有最大值?最大值是多少?
(3)保持t=2时的矩形ABCD不动,向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G,H,且直线GH平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
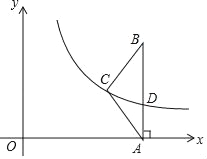
【题目】如图,在△ABC中,AC=BC=5,AB=8,AB⊥x轴,垂足为A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.
(x>0)的图象经过点C,交AB于点D.
(1)若OA=AB,求k的值;
(2)若BC=BD,连接OC,求△OAC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com