
【题目】我校开展的社团活动有:A.动漫社团;B.轮滑社团:C.音乐社团;D.诗歌社团;E.书法社团.学生管理中心为了了解全校500名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全
抽样调查:从七、八、九三个年级中随机抽取男女生各20名进行问卷调研;
收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B
A,C,E,D,B,A,B,E,C,A
D,D,B,B,C,C,A,A,E,B
C,B,D,C,A,C,C,A,C,E
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图
社团项目 | 划记 | 人数 |
A动漫社 |
| 8 |
B轮滑社 | ||
C音乐社 |
| 12 |
D诗歌社 | ||
E书法社 |
| 6 |
合计 | 40 | 40 |
分析数据、推断结论

(1)在扇形统计图中,“B轮滑社团”所在的扇形的圆心角等于 度;
(2)根据学生管理中心获得的样本数据,估计全校大约有 名同学选择D社团.
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据全等多边形的定义,我们把四个角,四条边分别相等的两个凸四边形叫做全等四边形,记作:四边形ABCD≌四边形A1B1C1D1
(1)若四边形ABCD≌四边形A1B1C1D1,已知AB3,BC4,ADCD5,B90,D 60,则A1D1 ,B1 , A1C1 (直接写出答案);
(2)如图 1,四边形 ABEF≌四边形CBED,连接AD交 BE于点O,连接F,求证:AOBFOE;
(3)如图 2,若ABA1B1,BCB1C1,CDC1D1,ADA1D1,BB1,求证:四边形ABCD≌四边形A1B1C1D1


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.

(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG//DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,求证四边形AGBD是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
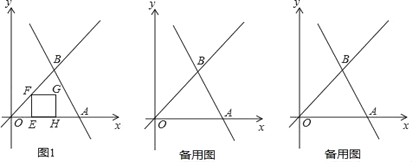
【题目】如图1,直线y=﹣2x+3与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为 ,∠AOB= ;
(2)求S△OAB的值;
(3)动点E从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点E作EF⊥x轴交直线y=x于点F,再以EF为边向右作正方形EFGH.设运动t秒时,正方形EFGH与△OAB重叠部分的面积为S.求:S与t之间的函数关系式,并写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com