
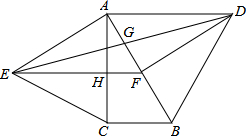
 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,下列结论不正确的是( )
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,下列结论不正确的是( )| A. | EF⊥AC | B. | AD=4AG | ||
| C. | 四边形ADEF为菱形 | D. | FH=$\frac{1}{4}$BD |
分析 根据已知先判断△ABC≌△EFA,则∠AEF=∠BAC,得出EF⊥AC,由等边三角形的性质得出∠BDF=30°,从而证得△DBF≌△EFA,则AE=DF,再由FE=AB,得出四边形ADFE为平行四边形而不是菱形,根据平行四边形的性质得出AD=4AG,从而得到答案.
解答 解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠FAE=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
∴△ABC≌△EFA,
∴FE=AB,
∴∠AEF=∠BAC=30°,
∴EF⊥AC,故A正确;
∵EF⊥AC,∠ACB=90°,
∴HF∥BC,
∵F是AB的中点,
∴HF=$\frac{1}{2}$BC,
∵BC=$\frac{1}{2}$AB,AB=BD,
∴HF=$\frac{1}{4}$BD,故D说法正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=∠BAC+∠CAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠AEF,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB,
∴四边形ADFE为平行四边形,
∵AE≠EF,
∴四边形ADFE不是菱形;
故C说法不正确;
∴AG=$\frac{1}{2}$AF,
∴AG=$\frac{1}{4}$AB,
∵AD=AB,
则AD=4AG,故B说法正确,
故选C.
点评 本题考查了菱形的判定和性质,以及全等三角形的判定和性质,解决本题需先根据已知条件先判断出一对全等三角形,然后按排除法来进行选择.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:填空题
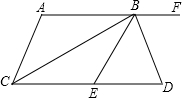 如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
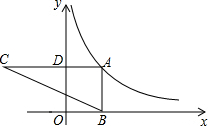 如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=2AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为4.
如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=2AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的直线必垂直于这条弦 | |
| B. | 垂直平分弦的直线必平分这条弦所对的弧 | |
| C. | 平分弦的直径必垂直于这条弦,并且平分这条弦所对的两条弧 | |
| D. | 垂直于弦的直线必过圆心 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
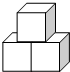 如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )
如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )| A. | 主视图的面积最大 | B. | 左视图的面积最大 | ||
| C. | 俯视图的面积最大 | D. | 三个视图的面积一样大 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个布袋中装有只有颜色不同的若干个球,分别是6个白球,b个黑球,红球和黄球的总数是黑球的两倍,红球数又是黄球的两倍,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整).
一个布袋中装有只有颜色不同的若干个球,分别是6个白球,b个黑球,红球和黄球的总数是黑球的两倍,红球数又是黄球的两倍,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com