练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．如图1反映的过程是：矩形ABCD中，动点P从点A出发，依次沿对角线AC、边CD、边DA运动至点A停止，设点P的运动路程为x，S△ABP=y．则矩形ABCD的周长是（　　）
    A．6B．12C．14D．15

    分析 由图2可以看出x=5时，点P到达C点，x=9时，点P到达D点，可求出CD的长，再根据勾股定理求出BC，即可求出矩形ABCD的周长．

    解答 解：由图2可以看出x=5时，点P到达C点，x=9时，点P到达D点，
    ∴AC=5，CD=9-5=4，
    根据勾股定理，BC=3，
    ∴矩形ABCD的周长=2（BC+CD）=2×（3+4）=14．
    故选：C．

    点评 本题主要考查了动点问题的函数图形，根据函数图形求出AC和CD的长度是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．[11b2-6b+13]-[9b2-9b+17]=2b2+3b+（-4）．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷（解析版） 题型：解答题

    计算

    （1）

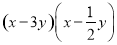
    （2）

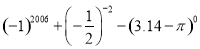
    （3）（1－3y）（1+3y）（1+9y2）

    （4）（ab+1）2－（ab－1）2

    （5）

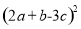
    （6）

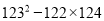
    查看答案和解析>>

    科目：初中数学 来源：2017届湖北省赤壁市九年级下学期第一次模拟（调研）考试数学试卷（解析版） 题型：解答题

    如图，在平面直角坐标系中，已知矩形ABCD的三个顶点A(－3，4)、B(－3，0)、C(－1，0) .以D为顶点的抛物线y = ax2+bx+c过点B. 动点P从点D出发，沿DC边向点C运动，同时动点Q从点B出发，沿BA边向点A运动，点P、Q运动的速度均为每秒1个单位，运动的时间为t秒. 过点P作PE⊥CD交BD于点E，过点E作EF⊥AD于点F，交抛物线于点G.

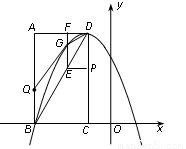
    （1）求抛物线的解析式；

    （2）当t为何值时，四边形BDGQ的面积最大？最大值为多少？

    （3）动点P、Q运动过程中，在矩形ABCD内（包括其边界）是否存在点H，使以B，Q，E，H为顶点的四边形是菱形，若存在，请直接写出此时菱形的周长；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

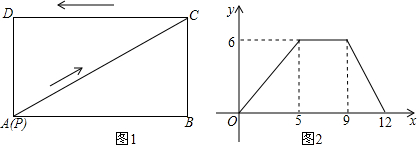
    5．某运动员在图所示的场地上匀速跑步，他从点A出发，沿箭头所示方向经过点B跑到点C，共用时30秒．他的教练选择了一个固定的位置Q观察他的跑步过程．设跑步的时间为t（单位：秒），他与教练的距离为y（单位：米）．下列能反映y与t的函数关系的大致图象是（　　）
    A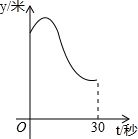．B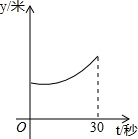．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

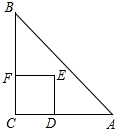    13．如图，Rt△ABC中，∠C=90°，AC=BC=2，正方形CDEF的顶点D、F分别在AB、BC边上，设CD的长度为x，△ABC与正方形CDEF重叠部分的面积为y，则下列图象能表示y与x之间的函数关系的是（　　）
    A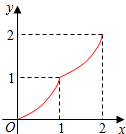．B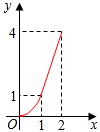．C．D．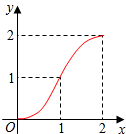

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

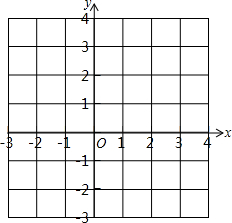    20．如图，已知O是坐标原点，A、B两点的坐标分别为（3，-1）、（2，1）．
    （1）以O点为旋转中心将△OAB逆时针旋转90°得到△OA′B′，画出旋转前与旋转后的图形；
    （2）如果△OAB内部一点M的坐标为（x，y），写出M的对应点M′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

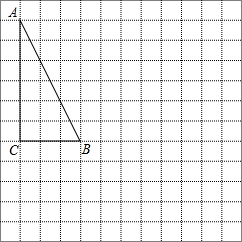    14．在下面的网格图中，每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，BC=3，AC=6．
    ①试作出△ABC以B为旋转中心，沿顺时针方向旋转90°后的图形△BA1C1；
    ②若点A的坐标为（-3，4），试建立合适的直角坐标系，并写出B，C两点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列分解因式正确的是（　　）
    A．x2+y2=（x+y）（x-y）B．m2-2m+1=（m+1）2C．（a+4）（a-4）=a2-16D．x3-x=x（x2-1）

    查看答案和解析>>

    同步练习册答案