Question

【题目】如图，在正方形ABCD中，AB=，E是对角线AC上的动点，以DE为边作正方形DEFG，H是CD的中点，连接GH，则GH的最小值为____．

Answer 1

【答案】

【解析】

由∠ADC=∠EDG=90°，推出∠ADE=∠CDG，连接GC，容易证明△DAE≌△DCG，推出AE=CG，当E点位于C点时，G点位于AD的延长线G1处，进而推出G点在CG1这条线段上运动，再由点到直线的距离垂线段最短知，过H向CG1作垂线，得到GH的最小值.

解：连接CG，如下图所示：

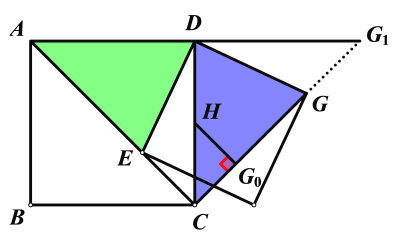
∵∠ADC=∠EDG=90°

∴∠ADC-∠EDC=∠EDG-∠EDC

∴∠ADE=∠CDG

在△ADE和△CDG中

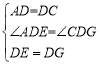，∴△ADE和△CDG(SAS)

∴AE=CG

当E点位于C点时，G点位于G1处

当E但位于A点时，G点位于C处，

故E点在AC上运动时，G点在CG1上运动

故由点到直线的距离垂线段最短可知：

过H点作HG0⊥CG时，此时HG0最小

又H是CD的中点，∴CH=CD=

又∠DCG=45°，

∴HG0=CH=.

故答案为：