
【题目】如图,在平面直角坐标系中,点A,C的坐标分别为(a,0),(0,b),点B在第一象限内,且a,b满足|a3﹣64|+![]() =0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
=0.点P从原点出发,以每秒2个单位长度的速度沿着长方形OABC的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).

(1)求点B的坐标;
(2)当点P移动4秒时,求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,请直接写出点P移动的时间t.
【答案】(1)点B的坐标为(4,6);(2)点P的坐标为(4,4);(3)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)根据非负数的性质分别求出a、b,得到点B的坐标;
(2)根据点P的运动时间求出运动距离,结合图形求出点P的坐标;
(3)分点P在OC上、点P在BA上两种情况,结合图形计算即可.
解:(1)由题意得,a3﹣64=0,b﹣6=0,
解得,a=4,b=6,
∴点A,C的坐标分别为(4,0),(0,6),
∵四边形OABC是矩形,
∴CB=OA=4,AB=OC=6,
∴点B的坐标为(4,6);
(2)∵点P从原点出发,以每秒2个单位长度的速度沿着O→C→B→A→O的路线移动,
∴点P移动的距离为2×4=8,
∵OA+AP=4+4=8,
∴点P在AB上,且距离点A4个单位长度,
∴点P的坐标为(4,4);
(3)当点P在OC上时,点P移动的时间为:(4+6+4+1)÷2=![]() (秒),
(秒),
当点P在BA上时,点P移动的时间为:(4+5)÷2=![]() (秒),
(秒),
答:点P到x轴的距离为5个单位长度时,求点P移动的时间为![]() 秒或
秒或![]() 秒.
秒.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】问题引入:
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() 下列说法:①当
下列说法:①当![]() 时,则方程
时,则方程![]() 一定有一根为
一定有一根为![]() ;②若
;②若![]() 则方程
则方程![]() 一定有两个不相等的实数根;③若
一定有两个不相等的实数根;③若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() ;④若
;④若![]() ,则方程
,则方程![]() 有两个不相等的实数根。其中正确的是( )
有两个不相等的实数根。其中正确的是( )
A.①②B.①③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,写出A、B的坐标:A_________、B________;
(2)如图1所示,将点A向右平移1个单位到点D,点C、B关于y轴对称,求出四边形ABCD的面积;
(3)将图1中的网格去掉得到图2所示,直线AB的交y轴于点C,直线CD⊥AB于点C,△ACD为等腰直角三角形,且∠ACD=90°,求点D的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A.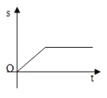 B.
B.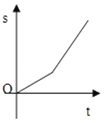 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥百货大厦某店卖一种狗宝宝布娃娃纪念品,已知成批购进时单价为4元,根据市场调查,销售量与销售单价在一段时间内满足如下关系:单价为10元时销售量为300枚,而单价每降低1元,就可多售出5枚,那么求可获得最大利润为__元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC≌△DEF,点B、E、C、F在同一直线上,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求∠F的度数与DH的长;
(2)求证:AB∥DE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com