练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．分解因式：（x-5）（3x-2）-3（x-5）=（x-5）（3x-5）．

    分析 将原式的公因式（x-5）提出即可得出答案．

    解答 解：（x-5）（3x-2）-3（x-5）
    =（x-5）（3x-2-3）
    =（x-5）（3x-5）．
    故答案为：（x-5）（3x-5）．

    点评 本题考查因式分解-提公因式法，因式分解的步骤为：一提公因式；二看公式．一般来说，如果可以提取公因式的要先提取公因式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

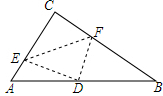    17．如图，在Rt△ABC中，∠C=90°，翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF（点E，F分别在边AC，BC上）．若△CEF与△ABC相似．
    （1）当AC=BC=2时，求AD的长；
    （2）当AC=3，BC=4时，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

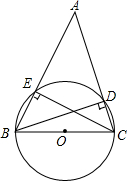    18．如图所示，BD、CE分别是△ABC的高．
    （1）求证：B、C、D、E四点在同一个圆上；
    （2）∠ABC=60°，CE=12，试求过B、C、D、E四点的圆的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知x2+y2=13，xy=6，
    求：（1）x+y；（2）x-y．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．分式的乘除混合运算
    （1）$\frac{3a{b}^{2}}{2{x}^{3}y}$•（-$\frac{8xy}{9{a}^{2}b}$）÷$\frac{3x}{（-4b）}$
    （2）$\frac{{y}^{2}-4y+4}{2y-6}$$•\frac{1}{y+3}$÷$\frac{12-6y}{9-{y}^{2}}$
    （3）$\frac{（x-y）^{2}}{（y-x）^{3}}$•（x-y）4÷$\frac{9}{y-x}$
    （4）（y-x）÷$\frac{{x}^{2}-2xy+{y}^{2}}{xy}$•$\frac{x-y}{{x}^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些土豆后，又降价出售，售出土豆的千克数与他手中持有钱数（含备用零钱）的关系如图所示，结合图象回答下列问题．
    （1）降价前他每千克土豆出售的价格是多少？
    （2）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含零用钱）比降价前全部售完少买了1.5元，问：他一共带了多少千克土豆？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．若x3-2x2+ax+b除以（x-2）（x+1）所得的余数为2x+1，则a、b的值为（　　）
    A．a=1，b=-3B．a=-1，b=-3C．a=-1，b=3D．a=1，b=3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．把下列各式分解因式：
    （1）9m2-15m+$\frac{25}{4}$；
    （2）（x2+1）2-4x2；
    （3）a3b-2a2b2+ab3；
    （4）（x+y）2-4（x+y-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

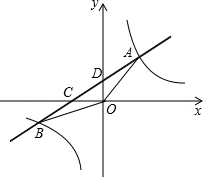    17．如图，在平面直角坐标系xOy中，一次函数y=$\frac{1}{2}$x+1的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于一、三象限内的A、B两点，直线AB与坐标轴交于C、D两点，△ADO的面积为2．
    （1）求反比例函数的解析式；
    （2）求△COB的面积．

    查看答案和解析>>

    同步练习册答案