
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.

【答案】(1)见解析;(2)AE=5.
【解析】
(1)依据矩形的性质,即可得出△AEG≌△CFH,进而得到GE=FH,∠CHF=∠AGE,由∠FHG=∠EGH,可得FH∥GE,即可得到四边形EGFH是平行四边形;
(2)由菱形的性质,即可得到EF垂直平分AC,进而得出AF=CF=AE,设AE=x,则FC=AF=x,DF=8-x,依据Rt△ADF中,AD2+DF2=AF2,即可得到方程,即可得到AE的长.
(1)∵矩形ABCD中,AB∥CD,
∴∠FCH=∠EAG,
又∵CD=AB,BE=DF,
∴CF=AE,
又∵CH=AG,
∴△AEG≌△CFH,
∴GE=FH,∠CHF=∠AGE,
∴∠FHG=∠EGH,
∴FH∥GE,
∴四边形EGFH是平行四边形;
(2)如图,连接EF,AF,

∵EG=EH,四边形EGFH是平行四边形,
∴四边形GFHE为菱形,
∴EF垂直平分GH,
又∵AG=CH,
∴EF垂直平分AC,
∴AF=CF=AE,
设AE=x,则FC=AF=x,DF=8-x,
在Rt△ADF中,AD2+DF2=AF2,
∴42+(8-x)2=x2,
解得x=5,
∴AE=5.


科目:初中数学 来源: 题型:
【题目】据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:
(1)由![]() ,因为
,因为![]() ,请确定
,请确定![]() 是______位数;
是______位数;
(2)由32768的个位上的数是8,请确定![]() 的个位上的数是________,划去32768后面的三位数768得到32,因为
的个位上的数是________,划去32768后面的三位数768得到32,因为![]() ,请确定
,请确定![]() 的十位上的数是_____________;
的十位上的数是_____________;
(3)已知![]() 和
和![]() 分别是两个数的立方,仿照上面的计算过程,请计算:
分别是两个数的立方,仿照上面的计算过程,请计算:![]() ;
;![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,A、B分别为直线
,A、B分别为直线![]() 、
、![]() 上两点,且
上两点,且![]() ,若射线
,若射线![]() 绕点顺时针旋转至
绕点顺时针旋转至![]() 后立即回转,射线
后立即回转,射线![]() 绕点B逆时针旋转至
绕点B逆时针旋转至![]() 后立即回转,两射线分别绕点A、点B不停地旋转,若射线
后立即回转,两射线分别绕点A、点B不停地旋转,若射线![]() 转动的速度是
转动的速度是![]() /秒,射线
/秒,射线![]() 转动的速度是
转动的速度是![]() /秒,且a、b满足
/秒,且a、b满足![]() .若射线
.若射线![]() 绕点A顺时针先转动18秒,射线
绕点A顺时针先转动18秒,射线![]() 才开始绕点B逆时针旋转,在射线
才开始绕点B逆时针旋转,在射线![]() 到达
到达![]() 之前,问射线
之前,问射线![]() 再转动_______秒时,射线
再转动_______秒时,射线![]() 与射线
与射线![]() 互相平行.
互相平行.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题
(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)请你对“不及格”等级的同学提一个友善的建议(一句话即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P为圆上一点,点C为AB延长线上一点,PA=PC,∠C=30°.
(1)求证:CP是⊙O的切线.
(2)若⊙O的直径为8,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?A,B两款手机的进货和销售价格如下表:
A款手机 | B款手机 | |
进货价格(元) | 1100 | 1400 |
销售价格(元) | 今年的销售价格 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 上的动点,且
上的动点,且![]() .
.
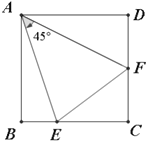
(1)如果将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() .请你画出图形(旋转后的辅助线).你能够得出关于
.请你画出图形(旋转后的辅助线).你能够得出关于![]() ,
,![]() ,
,![]() 的一个结论是________.
的一个结论是________.
(2)如果点![]() ,
,![]() 分别运动到
分别运动到![]() ,
,![]() 的延长线上,如图,请你能够得出关于
的延长线上,如图,请你能够得出关于![]() ,
,![]() ,
,![]() 的一个结论是________.
的一个结论是________.

(3)变式:如图,将题目改为“在四边形![]() 中,
中,![]() ,且
,且![]() ,点
,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 上的动点,且
上的动点,且![]() ”,请你猜想关于
”,请你猜想关于![]() ,
,![]() ,
,![]() 有什么关系?并验证你的猜想.
有什么关系?并验证你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN、MN,
(1)求证:△CMN是等边三角形;
(2)判断CN与⊙O的位置关系,并说明理由;
(3)若AD:AB=3:4,BN=4,求等边△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点A,C,D在⊙O上,过D作PF∥AC交⊙O于F,交AB于E,且∠BPF=∠ADC.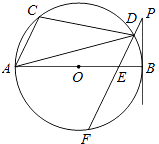
(1)判断直线BP和⊙O的位置关系,并说明你的理由;
(2)当⊙O的半径为 ![]() ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com