
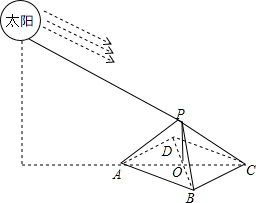
 某人设计了一种利用阳光下的影子测量金字塔高度的方法.他准备了皮尺、标杆等测量工具,并先行测得金字塔底座正方形ABCD的边长为100m,测量在太阳刚好到达AC所在直线正上方(但不在金字塔塔尖正上方)时进行(如图).
某人设计了一种利用阳光下的影子测量金字塔高度的方法.他准备了皮尺、标杆等测量工具,并先行测得金字塔底座正方形ABCD的边长为100m,测量在太阳刚好到达AC所在直线正上方(但不在金字塔塔尖正上方)时进行(如图).分析 (1)根据平行投影的概念画图即可;
(2)根据相似三角形的性质得到比例式,计算得到答案.
解答 解:(1)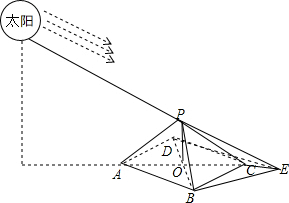 金字塔在地面的影子如图:
金字塔在地面的影子如图:
(2)∵正方形ABCD的边长为100m,
∴AC=100$\sqrt{2}$m,则OC=50$\sqrt{2}$m,
由题意得,$\frac{OP}{OE}$=$\frac{2}{5}$,即$\frac{OP}{50\sqrt{2}+90}$=$\frac{2}{5}$,
解得,OP=36+20$\sqrt{2}$≈64m,
答:这座金字塔的高度大约是64米.
点评 本题考查的是解直角三角形的应用,正确根据题意画出图形、灵活运用锐角三角函数的概念是解题的关键,注意相似三角形的性质在解题中的应用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
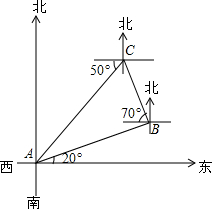 如图,一艘船由港口A出发向东偏北20°方向航行,这艘船航行的速度是每小时66海里,1小时后到达B处,发现一顶塔在西偏北79°方向,该船就朝灯塔驶去,到达灯塔后,发现港口在灯塔的西偏南50°方向,问灯塔与港口的距离是多少海里?
如图,一艘船由港口A出发向东偏北20°方向航行,这艘船航行的速度是每小时66海里,1小时后到达B处,发现一顶塔在西偏北79°方向,该船就朝灯塔驶去,到达灯塔后,发现港口在灯塔的西偏南50°方向,问灯塔与港口的距离是多少海里?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com