
【题目】正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
【答案】解:(1)垂直且相等。
(2)EF、EQ、BP三者之间的数量关系为:![]() 。
。
证明如下:
如图,取BC的中点G,连接FG,
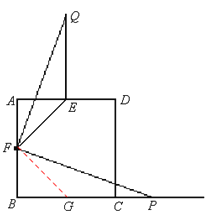
由(1)得EF=FG,EF⊥FG,
根据旋转的性质,FP=FQ,∠PFQ =90°。
∴∠GFP=∠GFE—∠EFP=90°—∠EFP,
∠EFQ=∠PFQ—∠EFP=90°—∠EFP。
∴∠GFP=∠EFQ。
在△FQE和△FPG中,∵EF=GF,∠EFQ=∠GFP,FQ = FP,
∴△FQE≌△FPG(SAS)。∴EQ=GP。
∴![]() 。
。
(3)补图如下,F、EQ、BP三者之间的数量关系为:![]() 。
。
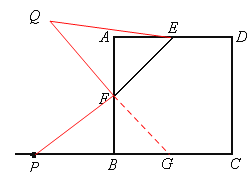
【解析】
试题分析:(1)EF与FG关系为垂直且相等(EF=FG且EF⊥FG)。证明如下:
∵点E、F、G分别是正方形边AD、AB、BC的中点,
∴△AEF和△BGD是两个全等的等腰直角三角形。
∴EF=FG,∠AFE=∠BFG=45°。∴∠EFG=90°,即EF⊥FG。
(2)取BC的中点G,连接FG,则由SAS易证△FQE≌△FPG,从而EQ=GP,因此![]() 。
。
(3)同(2)可证△FQE≌△FPG(SAS),得EQ=GP,因此,
![]() 。
。


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
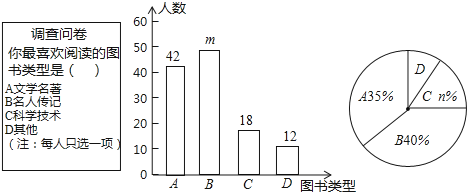
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合). 

(1)若BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D. ①若∠BAO=60°,则∠D=°.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由 .
(2)若∠ABC= ![]() ∠ABN,∠BAD=
∠ABN,∠BAD= ![]() ∠BAO,则∠D=°.
∠BAO,则∠D=°.
(3)若将“∠MON=90°”改为“∠MON=α(0°<α<180°)”,∠ABC= ![]() ∠ABN,∠BAD=
∠ABN,∠BAD= ![]() ∠BAO,其余条件不变,则∠D=°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=°(用含α、n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com