
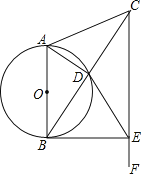
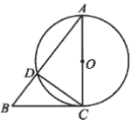
【题目】如图,在等腰△ABC中,AB=AC,以AB为直径的圆O交BC于点D,过点C作CF∥AB,与⊙O的切线BE交于点E,连接DE.
(1)求证:BD=CD;
(2)求证:△CAB∽△CDE;
(3)设△ABC的面积为S1,△CDE的面积为S2,直径AB的长为x,若∠ABC=30°,S1、S2 满足S1+S2=![]() ,试求x的值.
,试求x的值.
【答案】(1)详见解析;(2)详见解析;(3)x=8..
【解析】
(1)因为AB=AC,欲证明BD=DC,只要证明AD⊥BC即可.
(2)可以根据两角对应相等的两个三角形相似进行证明.
(3)分别用x表示S1、S2,列出方程即可解决问题.
(1)证明:∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD.
(2)∵AB∥CE,
∴∠2=∠1,
∵AB=AC,
∴∠1=∠3,
∵BE是⊙O切线,
∴∠ABE=90°,
∵AB∥CE,
∴∠BEC+∠ABE=90°,
∴∠BEC=90°,
∵BD=DC,
∴DE=DB=DC,
∴∠2=∠4,
∴∠3=∠2,∠1=∠4,
∴△CAB∽△CDE.
(3)∵S1=![]() .
.
∵△CAB∽△CDE,
∴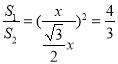 ,
,
∴S2=![]() ,
,
由题意:![]() ,
,
∴x=±8,
∵x>0,
∴x=8.



 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
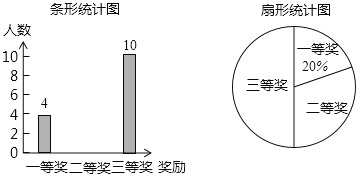
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)已知甲、乙、丙、丁4位同学获得一等奖,学校将采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”知识竞赛,请求出抽到的2人恰好是甲和乙的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE=![]() S△CEF.其中正确的是( )
S△CEF.其中正确的是( )
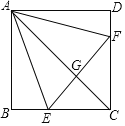
A. ①③B. ②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.

(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AC为直径的⊙O交AB于点D,连接CD,∠BCD=∠A.
(1)求证:BC是⊙O的切线;
(2)若BC=5,BD=3,求点O到CD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com