
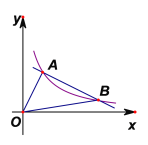
【题目】如图,在直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() ,
,![]() 、
、![]() ,
,![]() .连接
.连接![]() 、
、![]()
(1)求直线![]() 的解析式;
的解析式;
(2)若点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 为等腰三角形时,请直接写出点
为等腰三角形时,请直接写出点![]() 的坐标;
的坐标;
(3)求![]() 的面积.
的面积.
【答案】(1) ![]() ;(2)
;(2) 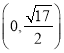 、
、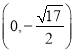 、
、![]() 、
、![]() ;(3)
;(3) ![]() .
.
【解析】
(1)先把![]() 、
、![]() 两点坐标代入反比例函数解析式即可求出
两点坐标代入反比例函数解析式即可求出![]() 、
、![]() 的值,进而可得出
的值,进而可得出![]() 、
、![]() 两点的坐标,再把
两点的坐标,再把![]() 、
、![]() 两点的坐标代入一次函数的关系式即可求出
两点的坐标代入一次函数的关系式即可求出![]() 、
、![]() 的值,进而可得出其关系式;
的值,进而可得出其关系式;
(2)设点C坐标为(0,y),由两点距离公式表示出求出AC,分三种情况(OA=OC、OC=AC、OA=AC)列方程求出y即可求出
(3)过A、B两点作x轴垂线垂足分别为H、G,根据![]() 计算即可;
计算即可;
解:(1)![]() 一次函数
一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于点
的图象相交于点![]() 、
、![]() ,
,
![]() 把
把![]() 点坐标代入反比例函数解析式得,
点坐标代入反比例函数解析式得,![]() ;
;
把![]() 点坐标代入反比例函数解析式得,
点坐标代入反比例函数解析式得,![]() ;
;
![]() 、
、![]() ,
,
代入一次函数![]() 得,
得,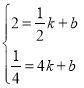 ,
,
解得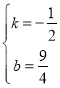 ,
,
![]() 一次函数的关系式为:
一次函数的关系式为:![]() ;
;
(2)设点![]() 坐标为
坐标为![]() ,则
,则![]() ,
,
∵![]() ,
,
∴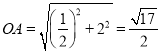 ,
,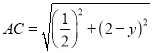 ,
,
![]() 为等腰三角形有三种情况:
为等腰三角形有三种情况:
当![]() 时,即
时,即![]() ,
,
解得:![]() ,即C点坐标为:
,即C点坐标为: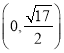 ,
, 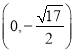 ;
;
当![]() 时,即
时,即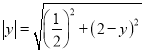 ,
,
解得:![]() ,即C点坐标为:
,即C点坐标为:![]() ;
;
当![]() 时,
时,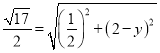 ,
,
解得:![]() 或
或![]() (舍去),故C点坐标为:
(舍去),故C点坐标为:![]() ;
;
综上所述,故C点坐标为: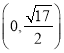 、
、 、
、![]() 、
、![]() .
.
(3)如图,过A、B两点作x轴垂线垂足分别为H、G,
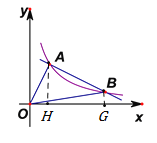
∴![]() ,
,
∵![]() ,
,
∴![]()


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上两点,且![]() ,连接OC,BD,OD.
,连接OC,BD,OD.
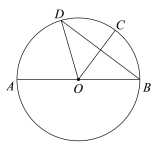
(1)求证:OC垂直平分BD;
(2)过点C作⊙O的切线交AB的延长线于点E,连接AD,CD.
①依题意补全图形;
②若AD=6,![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,直线
,直线![]() 与抛物线、
与抛物线、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() .
.
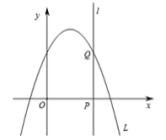
(1)![]() 时,
时,![]() 点的坐标为________;
点的坐标为________;
(2)当![]() 、
、![]() 两点重合时,求
两点重合时,求![]() 的值;
的值;
(3)当![]() 点达到最高时,求抛物线解析式;
点达到最高时,求抛物线解析式;
(4)在抛物线![]() 与
与![]() 轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出
轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出![]() 时“可点”的个数为____.
时“可点”的个数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
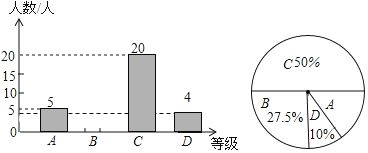
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
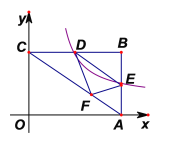
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,
轴上,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点,过点
边上一动点,过点![]() 的反比例函数
的反比例函数![]() 与边
与边![]() 交于点
交于点![]() .若将
.若将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点
的对应点![]() 恰好落在对角线
恰好落在对角线![]() 上. 则反比例函数的解析式是( )
上. 则反比例函数的解析式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
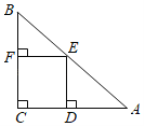
【题目】如图,在直角三角形![]() 中,
中,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 和
和![]() 的垂线,垂足分别为点
的垂线,垂足分别为点![]() 和点
和点![]() ,四边形
,四边形![]() 沿着
沿着![]() 方向以每秒
方向以每秒![]() 个单位的速度匀速运动,点
个单位的速度匀速运动,点![]() 与点
与点![]() 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为![]() ,运动过程中四边形
,运动过程中四边形![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() .则
.则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.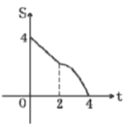 B.
B.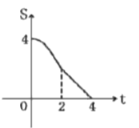
C.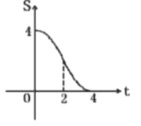 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
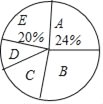
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
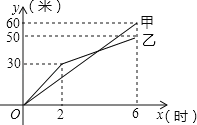
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com