
【题目】已知边长为5的菱形ABCD中,对角线AC长为6,点E在对角线BD上且tan∠EAC=![]() ,则BE的长为_____.
,则BE的长为_____.
【答案】3或5
【解析】
菱形ABCD中,边长为5,对角线AC长为6,由菱形的性质及勾股定理可得AC⊥BD,BO=4,分当点E在对角线交点左侧时(如图1)和当点E在对角线交点左侧时(如图2)两种情况求BE得长即可.
当点E在对角线交点左侧时,如图1所示:
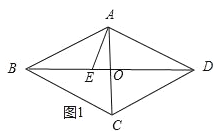
∵菱形ABCD中,边长为5,对角线AC长为6,
∴AC⊥BD,BO=![]() =4,
=4,
∵tan∠EAC=![]() ,
,
解得:OE=1,
∴BE=BO﹣OE=4﹣1=3,
当点E在对角线交点左侧时,如图2所示:
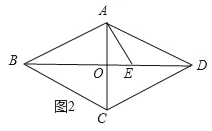
∵菱形ABCD中,边长为5,对角线AC长为6,
∴AC⊥BD,BO=![]() =4,
=4,
∵tan∠EAC=![]() ,
,
解得:OE=1,
∴BE=BO﹣OE=4+1=5,
故答案为:3或5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第________块.
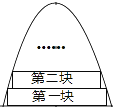
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).


查看答案和解析>>
科目:初中数学 来源: 题型:
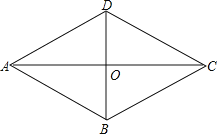
【题目】如图,在四边形ABCD中,AD∥BC,CA平分∠DCB,DB平分∠ADC
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求点D到AB的距离
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.
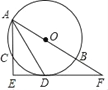
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数a,b,c(a<b<c)满足a2+b2=c2,则称(a,b,c)为一组“勾股数”.
观察下列两类“勾股数”:
第一类(a是奇数):(3,4,5);(5,12,13);(7,24,25);…
第二类(a是偶数):(6,8,10);(8,15,17);(10,24,26);…
(1)请再写出两组勾股数,每类各写一组;
(2)分别就a为奇数、偶数两种情形,用a表示b和c,并选择其中一种情形证明(a,b,c)是“勾股数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
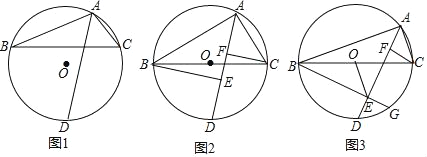
【题目】已知△ABC内接于⊙O,AD平分∠BAC.
(1)如图1,求证:![]() ;
;
(2)如图2,当BC为直径时,作BE⊥AD于点E,CF⊥AD于点F,求证:DE=AF;
(3)如图3,在(2)的条件下,延长BE交⊙O于点G,连接OE,若EF=2EG,AC=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线![]() 上有
上有![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() (单位:
(单位:![]() ).有一艘小船在点
).有一艘小船在点![]() 处,从
处,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向,从
的方向,从![]() 测得小船在北偏东
测得小船在北偏东![]() 的方向.
的方向.
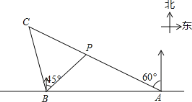
![]() 求点
求点![]() 到海岸线
到海岸线![]() 的距离;
的距离;
![]() 小船从点
小船从点![]() 处沿射线
处沿射线![]() 的方向航行一段时间后,到点
的方向航行一段时间后,到点![]() 处,此时,从
处,此时,从![]() 测得小船在北偏西
测得小船在北偏西![]() 的方向.求点
的方向.求点![]() 与点
与点![]() 之间的距离.(上述两小题的结果都保留根号)
之间的距离.(上述两小题的结果都保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,则△CEF的面积最大值是____.
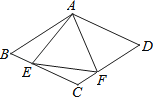
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com