
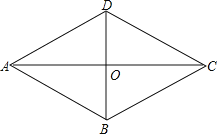
【题目】如图,在四边形ABCD中,AD∥BC,CA平分∠DCB,DB平分∠ADC
(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求点D到AB的距离
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由平行线的性质和角平分线的性质可得AD=BC,且AD∥BC,可证四边形ABCD是平行四边形,且AD=CD,可证四边形ABCD是菱形;
(2)由勾股定理可求AB的长,由面积法可求点D到AB的距离.
证明:(1)∵CA平分∠DCB,DB平分∠ADC
∴∠ADB=∠CDB,∠ACD=∠ACB
∵AD∥BC
∴∠DAC=∠ACB=∠ACD,∠ADB=∠DBC=∠CDB
∴AD=CD,BC=CD
∴AD=BC,且AD∥BC
∴四边形ABCD是平行四边形,且AD=CD
∴四边形ABCD是菱形
(2)如图,过点D作DE⊥AB,
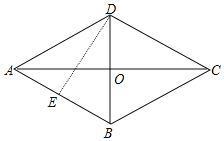
∵四边形ABCD是菱形
∴AO=CO=4,BO=DO=3,AC⊥BD
∴AB=![]() =
=![]() =5
=5
∵S△ABD=![]() AB×DE=
AB×DE=![]() ×DB×AO
×DB×AO
∴5DE=6×4
∴DE=![]()


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=6,∠ACB>90°,∠ABC的平分线交AC于点D,E是AB上一点,且BE=BC,CF∥ED交BD于点F,连接EF,ED.
(1)求证:四边形CDEF是菱形.
(2)当∠ACB= 度时,四边形CDEF是正方形,请给予证明;并求此时正方形的边长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市侯镇二中校园内有一荷花池,荷花池北侧有一水塔.九年级数学兴趣小组欲利用所学知识测量水塔高度.测量过程如下:先在荷花池南侧A点由测角仪AE测得塔顶仰角为30°,再在荷花池北侧B点由测角仪BF测得塔顶仰角为45°,荷花池AB长为15米,测角仪高均为1.5米,已知A、B、C三点在一条直线上,请根据以上条件求塔高CD?(保留两位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
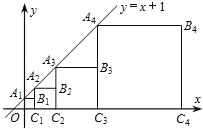
【题目】如图,直线 y=x+1 与 y 轴交于点 A1,以 OA1为边,在 y 轴右侧作正方形 OA1B1C1,延长 C1B1交直线 y=x+1 于点 A2,再以 C1A2为边作正方形,…,这些正方形与直线 y=x+1 的交点分别为 A1,A2,A3,…,An,则点 Bn 的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B. 在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C. 在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D. 在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com