
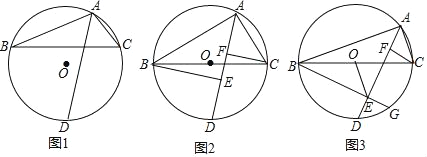
【题目】已知△ABC内接于⊙O,AD平分∠BAC.
(1)如图1,求证:![]() ;
;
(2)如图2,当BC为直径时,作BE⊥AD于点E,CF⊥AD于点F,求证:DE=AF;
(3)如图3,在(2)的条件下,延长BE交⊙O于点G,连接OE,若EF=2EG,AC=2,求OE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)2.
【解析】
(1)连接OB、OC、OD,根据圆心角与圆周角的性质得∠BOD=2∠BAD,∠COD=2∠CAD,又AD平分∠BAC,得∠BOD=∠COD,再根据圆周角相等所对的弧相等得出结论.
(2)过点O作OM⊥AD于点M,又一组角相等,再根据平行线的性质得出对应边成比例,进而得出结论;
(3)延长EO交AB于点H,连接CG,连接OA,BC为⊙O直径,则∠G=∠CFE=∠FEG=90°,四边形CFEG是矩形,得EG=CF,又AD平分∠BAC,再根据邻补角与余角的性质可得∠BAF=∠ABE,∠ACF=∠CAF,AE=BE,AF=CF,再根据直角三角形的三角函数计算出边的长,根据“角角边”证明出△HBO∽△ABC,根据相似三角形的性质得出对应边成比例,进而得出结论.
(1)如图1,连接OB、OC、OD,
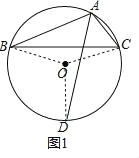
∵∠BAD和∠BOD是![]() 所对的圆周角和圆心角,
所对的圆周角和圆心角,
∠CAD和∠COD是![]() 所对的圆周角和圆心角,
所对的圆周角和圆心角,
∴∠BOD=2∠BAD,∠COD=2∠CAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠BOD=∠COD,
∴![]() =
=![]() ;
;
(2)如图2,过点O作OM⊥AD于点M,
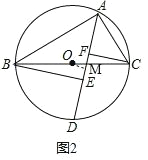
∴∠OMA=90°,AM=DM,
∵BE⊥AD于点E,CF⊥AD于点F,
∴∠CFM=90°,∠MEB=90°,
∴∠OMA=∠MEB,∠CFM=∠OMA,
∴OM∥BE,OM∥CF,
∴BE∥OM∥CF,
∴![]() =
=![]() ,
,
∵OB=OC,
∴![]() =
=![]() =1,
=1,
∴FM=EM,
∴AM﹣FM=DM﹣EM,
∴DE=AF;
(3)延长EO交AB于点H,连接CG,连接OA.
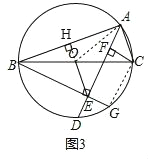
∵BC为⊙O直径,
∴∠BAC=90°,∠G=90°,
∴∠G=∠CFE=∠FEG=90°,
∴四边形CFEG是矩形,
∴EG=CF,
∵AD平分∠BAC,
∴∠BAF=∠CAF=![]() ×90°=45°,
×90°=45°,
∴∠ABE=180°﹣∠BAF﹣∠AEB=45°,
∠ACF=180°﹣∠CAF﹣∠AFC=45°,
∴∠BAF=∠ABE,∠ACF=∠CAF,
∴AE=BE,AF=CF,
在Rt△ACF中,∠AFC=90°,
∴sin∠CAF=![]() ,即sin45°=
,即sin45°=![]() ,
,
∴CF=2×![]() =
=![]() ,
,
∴EG=![]() ,
,
∴EF=2EG=2![]() ,
,
∴AE=3![]() ,
,
在Rt△AEB中,∠AEB=90°,
∴AB=![]() =
=![]() =6,
=6,
∵AE=BE,OA=OB,
∴EH垂直平分AB,
∴BH=EH=3,
∵∠OHB=∠BAC,∠ABC=∠ABC
∴△HBO∽△ABC,
∴![]() =
=![]() =
=![]() ,
,
∴OH=1,
∴OE=EH﹣OH=3﹣1=2.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
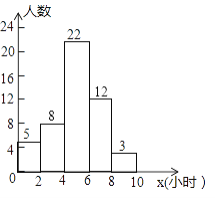
【题目】某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题
(1)本次接受随机抽样调查的学生人数为______;
(2)求这些学生每周课外体育活动时间的平均数________;
(3)估计全校学生每周课外体育活动时间不少于4小时的人数________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
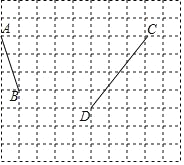
【题目】如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
(1)在方格纸中画出以AB为斜边的等腰直角三角形ABE,点E在小正方形的顶点上;
(2)在方格纸中画出以CD为对角线的矩形CMDN(顶点字母按逆时针顺序),且面积为10,点M、N均在小正方形的顶点上;
(3)连接ME,并直接写出EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
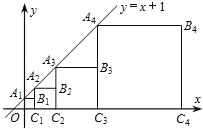
【题目】如图,直线 y=x+1 与 y 轴交于点 A1,以 OA1为边,在 y 轴右侧作正方形 OA1B1C1,延长 C1B1交直线 y=x+1 于点 A2,再以 C1A2为边作正方形,…,这些正方形与直线 y=x+1 的交点分别为 A1,A2,A3,…,An,则点 Bn 的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
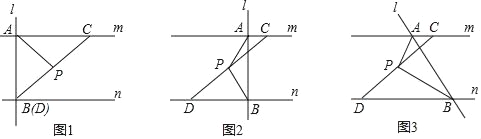
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,分别交m、n于点A、B,当点B与点D重合时(如图1),连结PA,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图1的情况下,把直线l向右平移到如图2的位置,试问(1)中的PA与PB
的关系式是否仍然成立?若成立,请给予证明;若不成立,请说明理由.
(3)延伸探究:在图2的情况下,把直线l绕点A旋转,使得∠APB=90°(如图3),若两平行线m、n之间的距离为2k,求证:PAPB=kAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.
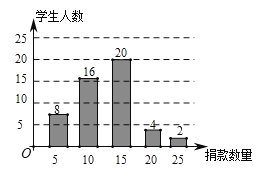
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com