
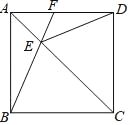
【题目】如图,在正方形ABCD中,E为对角线AC上一点,CE=CD,连接EB、ED,延长BE交AD于点F.求证:DF2=EFBF.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
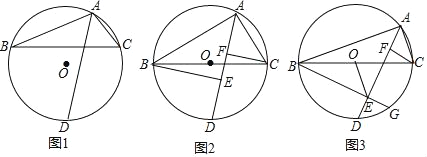
【题目】已知△ABC内接于⊙O,AD平分∠BAC.
(1)如图1,求证:![]() ;
;
(2)如图2,当BC为直径时,作BE⊥AD于点E,CF⊥AD于点F,求证:DE=AF;
(3)如图3,在(2)的条件下,延长BE交⊙O于点G,连接OE,若EF=2EG,AC=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若m2﹣2mn+2n2﹣10n+25=0,求m,n的值.
解:∵m2﹣2mn+2n2﹣10n+25=0,
∴(m2﹣2mn+n2)+(n2﹣10n+25)=0.
∴(m﹣n)2+(n﹣5)2=0,
∴m﹣n=0,n﹣5=0.
∴n=5,m=5.
根据你的观察,探究下面的问题:
(1)已知:x2+2xy+2y2+4y+4=0,求xy的值;
(2)已知:△ABC的三边长a,b,c都是正整数,且满足:a2+b2﹣16a﹣12b+100=0,求△ABC的周长的最大值;
(3)已知:△ABC的三边长是a,b,c,且满足:a2+2b2+c2﹣2b(a+c)=0,试判断△ABC是什么形状的三角形并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
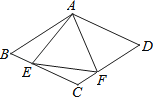
【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,则△CEF的面积最大值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
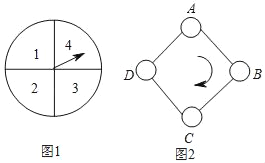
【题目】如图1,是一个材质均匀可自由转动的转盘,转盘的四个扇形面积相等,分别有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每转动转盘一次,当转盘停止运动时,指针所落扇形中的数字是几(当指针落在四个扇形的交线上时,重新转动转盘),就沿正方形的边顺时针方向连续跳几个边长.
如:若从图A起跳,第一次指针所落扇形中的数字是3,就顺时针连线跳3个边长,落到圈D;若第二次指针所落扇形中的数字是2,就从D开始顺时针续跳2个边长,落到圈B;……设游戏者从圈A起跳.
(1)嘉嘉随机转一次转盘,求落回到圈A的概率P1;
(2)琪琪随机转两次转盘,用列表法求最后落回到圈A的概率P2,并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
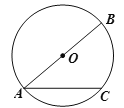
【题目】如图,AC是以AB为直径的⊙O的弦,点D是⊙O上的一点,过点D作⊙O的切线交直线AC于点E,AD平分∠BAE,若AB=10,DE=3,则AE的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a2b+c>0;④a+c>0,其中正确结论的个数为( )
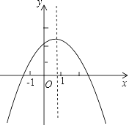
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com