
����Ŀ����ͼ������ABCD�ı߳�Ϊ2cm����DAB=60�㣮��P��A��������� ![]() cm/s���ٶȣ���AC��C�������˶������ͬʱ����QҲ��A���������1cm/s���ٶȣ�������AB�������˶�����P�˶���C��ʱ��P��Q��ֹͣ�˶������P�˶���ʱ��Ϊts��
cm/s���ٶȣ���AC��C�������˶������ͬʱ����QҲ��A���������1cm/s���ٶȣ�������AB�������˶�����P�˶���C��ʱ��P��Q��ֹͣ�˶������P�˶���ʱ��Ϊts�� 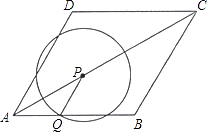
��1����P����A��Cʱ����˵��PQ��BC��
��2����PΪԲ�ġ�PQ��Ϊ�뾶��Բ�����ʣ��������˶������У�tΪ������ֵʱ����P���BC�ֱ���1���������2�������㣿
���𰸡�
��1���⣺���ı���ABCD�����Σ�������ABCD�ı߳�Ϊ2cm��
��AB=BC=2����BAC= ![]() ��DAB��
��DAB��
�֡ߡ�DAB=60�㣨��֪����
���BAC=��BCA=30�㣻
��ͼ1������BD��AC��O��
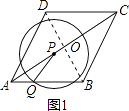
���ı���ABCD�����Σ�
��AC��BD��OA= ![]() AC��
AC��
��OB= ![]() AB=1��30������Ե�ֱ�DZ���б�ߵ�һ�룩��
AB=1��30������Ե�ֱ�DZ���б�ߵ�һ�룩��
��OA= ![]() ��cm����AC=2OA=2
��cm����AC=2OA=2 ![]() ��cm����
��cm����
�˶�ts�� ![]() ��
��
�� ![]()
�֡ߡ�PAQ=��CAB��
���PAQ�ס�CAB��
���APQ=��ACB�����������εĶ�Ӧ����ȣ���
��PQ��BC��ͬλ����ȣ���ֱ��ƽ�У�
��2���⣺��ͼ2����P��BC���ڵ�M������PM����PM��BC��

��Rt��CPM�У��ߡ�PCM=30�㣬��PM= ![]() PC=
PC= ![]()
��PM=PQ=AQ=t���� ![]() =t
=t
���t=4 ![]() ��6����ʱ��P���BC��һ�������㣻
��6����ʱ��P���BC��һ�������㣻
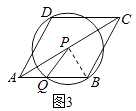
��ͼ3����P����B����ʱPQ=PB��
�ߡ�PQB=��PAQ+��APQ=60��
���PQBΪ�ȱ������Σ���QB=PQ=AQ=t����t=1
�� ![]() ʱ����P���BC��2�������㣮
ʱ����P���BC��2�������㣮
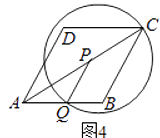
��ͼ4����P����C����ʱPC=PQ����2 ![]() t=t����t=3��
t=t����t=3�� ![]() ��
��
�൱1��t��3�� ![]() ʱ����P���BC��һ�������㣬
ʱ����P���BC��һ�������㣬
����P�˶�����C����t=2ʱP��C�غϣ�Q��B�غϣ�Ҳֻ��һ�����㣬��ʱ����P���BC��һ�������㣬
�൱t=4 ![]() ��6��1��t��3��
��6��1��t��3�� ![]() ��t=2ʱ����P������ABCD�ı�BC��1�������㣻
��t=2ʱ����P������ABCD�ı�BC��1�������㣻
��4 ![]() ��6��t��1ʱ����P���BC��2�������㣮
��6��t��1ʱ����P���BC��2�������㣮
����������1������BD��AC��O������ֱ��������AOB���������εĶԽ����ഹֱ���Խ���ƽ�ֶԽǡ��ڱ���ȵ�������֪��PAQ�ס�CAB��Ȼ����ݡ����������εĶ�Ӧ����ȡ�֤�á�APQ=��ACB��������ƽ���ߵ��ж�������ͬλ����ȣ���ֱ��ƽ�С�����֤�ý��ۣ���2����ͼ2����P��BC���ڵ�M������PM������Rt��CPM����Rt��CPM��������ǵ����Ǻ���ֵ���PM= ![]() PC=
PC= ![]() ��Ȼ�����PM=PQ=AQ=t�г�����t�ķ��̣�ͨ���ⷽ�̼������t��ֵ��
��Ȼ�����PM=PQ=AQ=t�г�����t�ķ��̣�ͨ���ⷽ�̼������t��ֵ��
��ͼ3����P����B����ʱPQ=PB�����ݵȱ������ε��ж�������֪��PQBΪ�ȱ������Σ�Ȼ���ɵȱ������ε������Լ���2�������t��ֵ��ȷ����ʱt��ȡֵ��Χ��
��ͼ4����P����C����ʱPC=PQ���ݴ˵�����ϵ�г�����t�ķ��̣�ͨ���ⷽ�����t��ֵ��
�����㾫����������Ĺؼ������������ε����ʵ����֪ʶ���������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룬�Լ���ֱ����Բ������λ�ù�ϵ�����⣬�˽�ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е㣮


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ħ�г���һ���ϱ������Ѳ�ߣ�ij�����Ӹ�ͤ����������ͣ����A�����涨����Ϊ����������ʻ�����¼���£���λ��ǧ�ף���+10��-8��+7��-15��+6��-16��+4��-2��+9.
��1��A���ڸ�ͤ�η��������ͤ��Զ��
��2����Ħ�г�ÿ��ʻ1ǧ����0.5������һ�칲���Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ�ABC�У���ACB=90�㣬��B=30�㣬AC=2 ![]() �����ǰ���ֱ�Ƕ���C��ʱ����ת������A�Ķ�Ӧ��A������AB�ߵ���ʼλ����ʱ��ֹͣת������B��ת����·����Ϊ�� ��
�����ǰ���ֱ�Ƕ���C��ʱ����ת������A�Ķ�Ӧ��A������AB�ߵ���ʼλ����ʱ��ֹͣת������B��ת����·����Ϊ�� �� 
A.![]() ��
��
B.![]() ��
��
C.2��
D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר��������A��B�����ͺŵ�����Դ�����������۳�1��A�ͳ���3��B�ͳ������۶�Ϊ96��Ԫ����������2��A�ͳ���1��B�ͳ������۶�Ϊ62��Ԫ��
��1����ÿ��A�ͳ���B�ͳ����ۼ۸�������Ԫ��
��2����˾����õ깺��A��B�����ͺŵ�����Դ������6���������Ѳ�����130��Ԫ���Ҳ�����140��Ԫ. �����ļ��ֹ�������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵���ѧ���������������˽�̶ȣ�ijУ��ѧ��������һ�γ������飬����������Ϊ�ĸ��ȼ���A���dz��˽⣻B���Ƚ��˽⣻C�������˽⣻D�����˽⣮���ݵ���ͳ�ƽ������������ͼ��ʾ�IJ�����������ͳ��ͼ����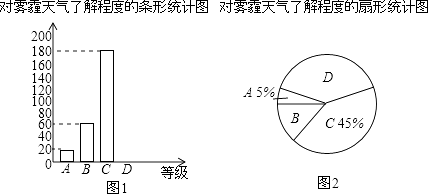
���������˽�̶� | �ٷֱ� |
A���dz��˽� | 5% |
A���Ƚ��˽� | 15% |
C�������˽� | 45% |
D�����˽� | n |
����ͳ��ͼ�����ش��������⣺
��1�����β�������ѧ�������ˣ�n=������ͳ��ͼ��D������������Ӧ��Բ�Ľ����ȣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ݵ�������ѧУ����չ����������֪ʶ������ij��Ҫ�ӡ��dz��˽⡱�̶ȵ�С����С����ѡһ�˲μӣ��������������Ϸ��ȷ������������ǣ����ĸ���ȫ��ͬ��ƹ�����������1��2��3��4��Ȼ��ŵ�һ�������Ĵ��У�һ�����ȴӴ����������һ������һ���ٴ�ʣ�µ����������������һ�������������������ϵ����ֺ�Ϊ��������С��ȥ������С��ȥ��������״ͼ���б���˵�������Ϸ�����Ƿ�ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AM��BN����A=60������P������AM��һ���㣨���A���غϣ���BC��BD�ֱ�ƽ�֡�ABP�͡�PBN���ֱ�����AM�ڵ�C��D��
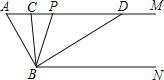
��1�����CBD�Ķ�����
��2������P�˶�ʱ����APB����ADB�ı�ֵ�Ƿ���֮�仯�������䣬����������ֵ�����仯�����ҳ��仯���ɣ�
��3������P�˶���ij��ʱ����ACB=��ABD�����ʱ��ABC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ͬһ��·��˳������������A��B��C���ס��������οʹӾ���A�������ײ��е�����C���һ�20����ʱ���ŶӺ�˹۹�ȵ�����B����B��ͣ��һ��ʱ����ٲ��е�����C���ס��������뾰��A��·��s���ף�����ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ��
��1�����ٶ��� ��/���ӣ�
��2����20��t ��30ʱ�������뾰��A��·��s��t�ĺ�������ʽ��
��3���ҳ�����ʱ�������;��������
��4���������ᄚ��Cʱ�����뾰��C��·��Ϊ360�ף����ҴӾ���B���е�����C���ٶ��Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���BAC=90�㣬AB=AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ����AD�Ҳ���������ADEF������CF��
��1���۲����
��ͼ1������D���߶�BC��ʱ��
��BC��CF��λ�ù�ϵΪ�� ��
��BC��CD��CF֮���������ϵΪ������������ֱ��д�ں����ϣ�
��2����ѧ˼��
��ͼ2������D���߶�CB���ӳ�����ʱ�����ۢ٣����Ƿ���Ȼ�������������������֤������������������д����ȷ�����ٸ���֤����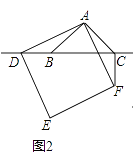
��3����չ����
��ͼ3������D���߶�BC���ӳ�����ʱ���ӳ�BA��CF�ڵ�G������GE������֪AB=2 ![]() ��CD=
��CD= ![]() BC�������GE�ij���
BC�������GE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P�ǵȱ�������ABC�ڵ�һ�㣬����PA��PB��PC����BPΪ������PBQ=60�㣬��BQ=BP������CQ.��PA��PB��PC=3��4��5������PQ�����жϡ�PQC����״�� ��

A. ֱ�������� B. ���������� C. ��������� D. �۽�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com