
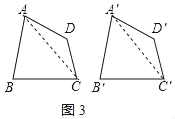
【题目】阅读下面材料,完成相应的任务:

(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形,由此判断命题①是 命题(填“真”或“假”);
(2)小彬经过探究发现命题②是真命题,请你结合图2证明这一命题;
(3)小颖经过探究又提出了一个新的命题:“若AB=A′B′,BC=B′C′,CD=C′D' , ,则四边形ABCD≌四边形A′B′C′D′,请在横线上填写两个关于“角”的条件,使该命题为真命题.
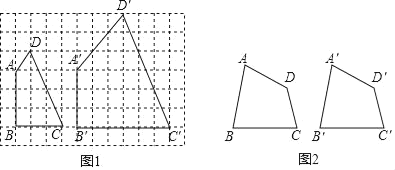
【答案】(1)假;(2)证明见解析;(3)∠B=∠B′,∠C=∠C′.
【解析】
(1)连接AC,延长BC到E,过点E作EF∥CD,交AD的延长线于点F,则∠E=∠BCD,∠F=∠ADC,将四边形ABEF平移得到四边形A′B′C′D′,则AB=A′B′,∠A=∠A′,∠B=∠B′,∠C=∠C′,∠D=∠D′,而BC≠B′C′,AD≠A′D′,得出四边形ABCD和四边形A′B′C′D′不全等,即可得出结论;
(2)连接BD,B′D′,证明△ABD≌△A′B′D′,得出BD=B′D′,∠ABD=∠A′B′D′,∠ADB=∠A′D′B′,再证明△BCD≌△B′C′D′,得出∠C=∠C′,∠CBD=∠C′B′D′,∠BDC=∠B′D′C′,证出∠ABC=∠A′B′C′,∠CDA=∠C′D′A′,即可得出结论;
(3)连接AC、A′C′,证明△ABC≌△A′B′C′,得出AC=A′C′,∠BAC=∠B′A′C′,∠BCA=∠B′C′A′,得出∠ACD=∠A′C′D′,再证明△ACD≌△A′C′D′,得出AD=A′D′,∠D=∠D′,∠CAD=∠C′A′D′,证出∠BAD=∠B′A′D′,即可得出结论.
解:(1)连接AC,延长BC到E,过点E作EF∥CD,交AD的延长线于点F,
则∠E=∠BCD,∠F=∠ADC,
将四边形ABEF平移得到四边形A′B′C′D′,如图1所示:
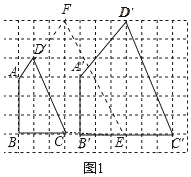
则AB=A′B′,∠A=∠A′,∠B=∠B′,∠C=∠C′,∠D=∠D′,
而BC≠B′C′,AD≠A′D′,
∴四边形ABCD和四边形A′B′C′D′不全等,
∴命题①是假命题,
故答案为:假;
(2)证明:连接BD,B′D′,如图2所示:
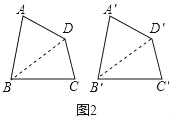
在△ABD和△A′B′D′中,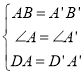
∴△ABD≌△A′B′D′(SAS),
∴BD=B′D′,∠ABD=∠A′B′D′,∠ADB=∠A′D′B′,
在△BCD和△B′C′D′中,
∴△BCD≌△B′C′D′(SSS),
∴∠C=∠C′,∠CBD=∠C′B′D′,∠BDC=∠B′D′C′,
∵∠ABC=∠ABD+∠CBD,∠A′B′C′=∠A′B′D′+∠C′B′D′,∠CDA=∠ADB+∠BDC,∠C′D′A′=∠A′D′B′+∠B′D′C′,
∴∠ABC=∠A′B′C′,∠CDA=∠C′D′A′,
∴四边形ABCD≌四边形A′B′C′D′;
(3)若AB=A′B′,BC=B′C′,CD=C′D',∠B=∠B′,∠C=∠C′,则四边形ABCD≌四边形A′B′C′D′;理由如下:
连接AC、A′C′,如图3所示:
在△ABC和△A′B′C′中,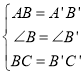
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠BAC=∠B′A′C′,∠BCA=∠B′C′A′,
∵∠C=∠C′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D′中,
∴△ACD≌△A′C′D′(SAS),
∴AD=A′D′,∠D=∠D′,∠CAD=∠C′A′D′,
∵∠BAD=∠BAC+∠CAD,∠B′A′D′=∠B′A′C′+∠C′A′D′,
∴∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′,
故答案为:∠B=∠B′,∠C=∠C′.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 为
为![]() 直径,点
直径,点![]() 为
为![]() 上一点,弦
上一点,弦![]() ,垂足为
,垂足为![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
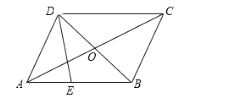
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为边AB上一点,且BE = 2AE.设![]() ,
,![]() .
.
(1)填空:向量![]() ;
;
(2)如果点F是线段OC的中点,那么向量![]() ,并在图中画出向量
,并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
注:本题结果用向量![]() 的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
查看答案和解析>>
科目:初中数学 来源: 题型:
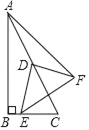
【题目】如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,BC=2,点D是AC边的中点,E是直线BC上一动点,将线段DE绕点D逆时针旋转90°得到线段DF,连接AF、EF,在点E的运动过程中线段AF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
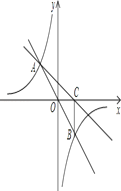
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式.
(3)点P在双曲线上,且△POC的面积等于△ABC面积的![]() ,求点P的坐标。
,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
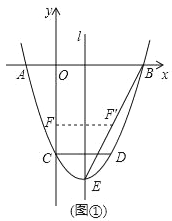
【题目】如图,二次函数y=x2+bx+c的图象与x轴交于 A、B两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b、c的值;
(2)如图①,连接BE,线段OC上的点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;
(3)如图②,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
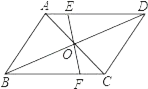
【题目】如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:如图2,
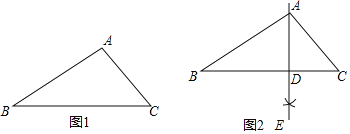
(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.所以线段AD就是所求作的高.
请回答:该尺规作图的依据是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com