
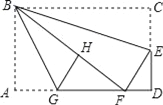
【题目】已知:![]() 为
为![]() 直径,点
直径,点![]() 为
为![]() 上一点,弦
上一点,弦![]() ,垂足为
,垂足为![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
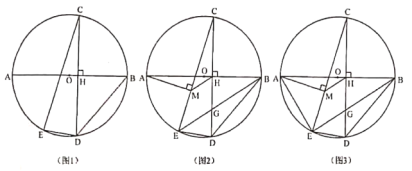
(1)如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)详见解析;(2)详见解析;(3)![]() 半径为
半径为![]() .
.
【解析】
(1)由AB为直径,CD⊥AB,得![]() ,从而∠CEB=∠BED=∠CDB,即可得到∠CED=2∠CDB,结合∠CDE=2∠CDB,即可求解;
,从而∠CEB=∠BED=∠CDB,即可得到∠CED=2∠CDB,结合∠CDE=2∠CDB,即可求解;
(2)由![]() 可得∠ACE=∠ABE,由AM⊥CE,CH⊥AB,可得∠AHC=∠AMC,则∠AHM=∠ACM,故∠AHM=∠ABE,即可求解;
可得∠ACE=∠ABE,由AM⊥CE,CH⊥AB,可得∠AHC=∠AMC,则∠AHM=∠ACM,故∠AHM=∠ABE,即可求解;
(3)证明△AEF≌△AEM(AAS)、△AFD≌△AMC(AAS)、△CGB∽△ECB,即可求解.
(1)∵![]() 为直径,
为直径,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
则∠AHM=∠ACM,
∴∠AHM=∠ABE,
∴MH∥BE;
(3)连接![]() 、
、![]() 、
、![]() ,过
,过![]() 作
作![]() ,
,
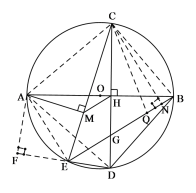
则![]() ,AE=AE,
,AE=AE,
∴![]() (AAS),
(AAS),
∴![]() ,EF=EM,
,EF=EM,
∵![]() 为直径,
为直径,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (HL) ,
(HL) ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
相似比![]() ,
,
∴设![]() ,
,![]() ,
,![]() ,
,
过点![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,
作![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() 半径为
半径为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
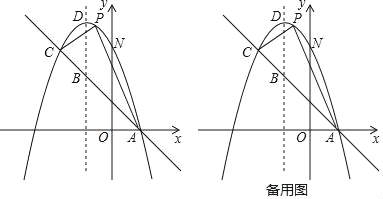
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
①甲种作物受环境影响最小;②乙种作物平均成活率最高;
③丙种作物最适合播种在山腰;
④如果每种作物只能在一个地方播种,那么山脚,山腰和山顶分别播种甲,乙,丙三种作物能使得成活率最高.其中合理的是( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型文体活动需招募一批学生作为志愿者参与服务,已知报名的男生有420人,女生有400人,他们身高均在![]() 之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
之间,为了解这些学生身高的具体分别情况,从中随机抽取若干学生进行抽样调查,抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表:
组别 | 身高(cm) |
A |
|
B |
|
C |
|
D |
|
E |
|
根据图表提供的信息,有下列几种说法
①估计报名者中男生身高的众数在D组;
②估计报名者中女生身高的中位数在B组;
③抽取的样本中,抽取女生的样本容量是38;
④估计身高在![]() 至
至![]() (不含
(不含![]() )的学生约有400人
)的学生约有400人
其中合理的说法是( )
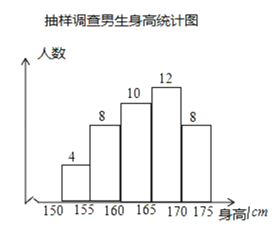
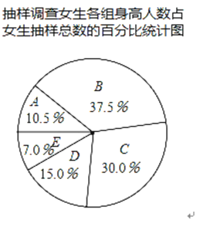
A.①②B.①④C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是等边三角形,以点C为旋转中心,将线段CA按顺时针方向旋转
是等边三角形,以点C为旋转中心,将线段CA按顺时针方向旋转![]() 得到线段CD,连接BD交AC于点O.
得到线段CD,连接BD交AC于点O.
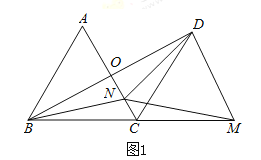
(1)如图1.
①求证:AC垂直平分BD;
②点M在BC的延长线上,点N在线段CO上,且![]() ,连接BN,判断
,连接BN,判断![]() 的形状,并加以证明;
的形状,并加以证明;
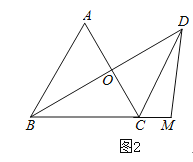
(2)如图2,点M在BC的延长线上,点N在线段AO上,且![]() ,补全图2,求证:
,补全图2,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
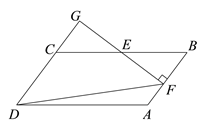
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°;②△DEF∽△ABG;③S△ABG=![]() S△FGH;④AG+DF=FG.
S△FGH;④AG+DF=FG.
其中正确的是__.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成相应的任务:

(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形,由此判断命题①是 命题(填“真”或“假”);
(2)小彬经过探究发现命题②是真命题,请你结合图2证明这一命题;
(3)小颖经过探究又提出了一个新的命题:“若AB=A′B′,BC=B′C′,CD=C′D' , ,则四边形ABCD≌四边形A′B′C′D′,请在横线上填写两个关于“角”的条件,使该命题为真命题.
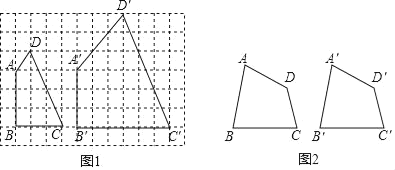
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com