
【题目】在平面直角坐标系![]() 中,对于任意三点
中,对于任意三点![]() ,
,![]() ,
,![]() 给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且
给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且![]() ,
,![]() ,
,![]() 三点都在矩形的内部或边界上,那么称该矩形为点
三点都在矩形的内部或边界上,那么称该矩形为点![]() ,
,![]() ,
,![]() 的外延矩形,在点
的外延矩形,在点![]() ,
,![]() ,
,![]() 所有的外延矩形中,面积最小的矩形称为点
所有的外延矩形中,面积最小的矩形称为点![]() ,
,![]() ,
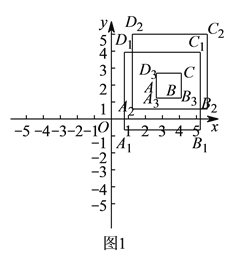
,![]() 的最佳外延矩形.例如,图
的最佳外延矩形.例如,图![]() 中的矩形
中的矩形![]() ,
,![]() ,
,![]() 都是点
都是点![]() ,
,![]() ,
,![]() 的外延矩形,矩形
的外延矩形,矩形![]() 是点
是点![]() ,
,![]() ,
,![]() 的最佳外延矩形.
的最佳外延矩形.
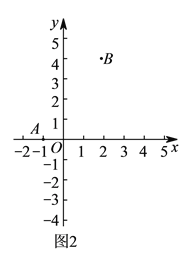
(![]() )如图
)如图![]() ,点
,点![]() ,
,![]() ,
,![]() (
(![]() 为整数).
为整数).
①如果![]() ,则点
,则点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是__________.
的最佳外延矩形的面积是__________.
②如果点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是
的最佳外延矩形的面积是![]() ,且使点
,且使点![]() 在最佳外延矩形的一边上,请写出一个符合题意的
在最佳外延矩形的一边上,请写出一个符合题意的![]() 值__________.
值__________.
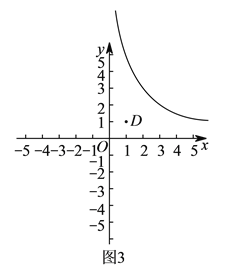
(![]() )如图
)如图![]() ,已知点
,已知点![]() 在函数
在函数![]() 的图象上,且点
的图象上,且点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积
的最佳外延矩形的面积![]() 的取值范围以及该面积最小时
的取值范围以及该面积最小时![]() 的取值范围.
的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
查看答案和解析>>
科目:初中数学 来源: 题型:
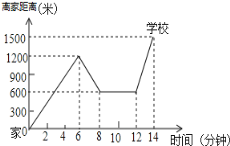
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米;
(2)小明在书店停留了多少分钟;
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4![]() ,
, ![]()
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,求证:四边形ABFC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A. 1个B. 2个C. 3个D. 3个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
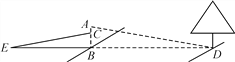
【题目】某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com