
【题目】在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C (0,3),点P在该抛物线的对称轴上,且纵坐标为2![]() .
.
(1)求抛物线的表达式以及点P的坐标;
(2)当三角形中一个内角α是另一个内角β的两倍时,我们称α为此三角形的“特征角”.
①当D在射线AP上,如果∠DAB为△ABD的特征角,求点D的坐标;
②点E为第一象限内抛物线上一点,点F在x轴上,CE⊥EF,如果∠CEF为△ECF的特征角,求点E的坐标.
【答案】(1)y=﹣x2+2x+3;点P(1,2![]() );(2)①D(0,
);(2)①D(0,![]() )或(3,4
)或(3,4![]() );②点E(
);②点E(![]() ,
,![]() ).
).
【解析】
(1)抛物线y=﹣x2+bx+c与y轴交于点C (0,3),则c=3,将点A的坐标代入抛物线表达式并解得:b=2,即可求解;
(2)①当α=60°,∠DBA=β![]() =30°时,△ABD为直角三角形,即可求解;当∠ADB=β时,则∠ABD=90°,即可求解;
=30°时,△ABD为直角三角形,即可求解;当∠ADB=β时,则∠ABD=90°,即可求解;
②∠CEF为△ECF的特征角,则△CEF为等腰直角三角形,则△CNE≌△EMF(AAS),即可求解.
解:
(1)∵抛物线y=﹣x2+bx+c与y轴交于点C(0,3),则c=3,
将点A的坐标代入抛物线表达式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+3;
点P(1,2![]() );
);
(2)由点A、P的坐标知,∠PAB=60![]() ,
,
直线AP的表达式为:y=![]() (x+1)…①,
(x+1)…①,
当α=60![]() ,∠DBA=β
,∠DBA=β![]() =30
=30![]() 时,
时,
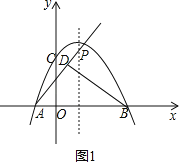
△ABD为直角三角形,由面积公式得:
yD×AB=ADBD,即yD×4=2×2![]() ,
,
解得:yD=![]() ,
,
点D在AP上,故点D(0,![]() );
);
当∠ADB=β时,则∠ABD=90![]() ,
,
故点D(3,4![]() );
);
综上,点D的坐标为:(0,![]() )或(3,4
)或(3,4![]() );
);
(3)∠CEF为△ECF的特征角,则△CEF为等腰直角三角形,
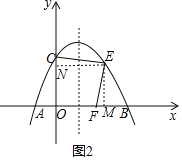
过点E分别作x轴、y轴的垂线交于点M、N,
则△CNE≌△EMF(AAS),
则EN=EM,即x=y,
x=y=﹣x2+2x+3,解得:x=![]() ;
;
故点E(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气给人们的生活带来很大影响,空气质量问题备受人们关注,为了减少雾霾影响,某单位计划为职工购买![]() 、
、![]() 两种型号的防霾口罩.已知每个
两种型号的防霾口罩.已知每个![]() 种型号防霾口罩价格比每个
种型号防霾口罩价格比每个![]() 种型号防霾口罩价格多
种型号防霾口罩价格多![]() 元,花
元,花![]() 元购买
元购买![]() 种型号防霾口罩和花
种型号防霾口罩和花![]() 元购买
元购买![]() 种型号防霾口罩的数量相同.
种型号防霾口罩的数量相同.
(1)求![]() 、
、![]() 两种型号防霾口罩每个价格各多少元?
两种型号防霾口罩每个价格各多少元?
(2)根据单位实际情况,需购买![]() 、
、![]() 两种型号防霾口罩共
两种型号防霾口罩共![]() 个,总费用不高于
个,总费用不高于![]() 万元,求
万元,求![]() 种型号防霾口罩至少要购买多少个?
种型号防霾口罩至少要购买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
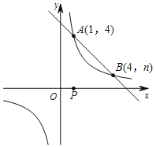
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践:如图△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O.
(2)以O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是_____ .(直接写出答案)
(2)若AC=5,BC=12,求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
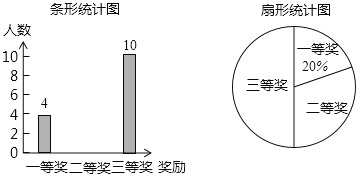
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)已知甲、乙、丙、丁4位同学获得一等奖,学校将采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”知识竞赛,请求出抽到的2人恰好是甲和乙的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
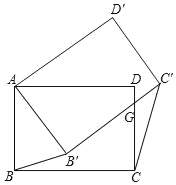
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转一定角度后,BC的对应边B′C交CD边于点G,如果当AB′=B′G时量得AD=7,CG=4,连接BB′、CC′,那么![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
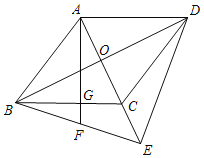
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
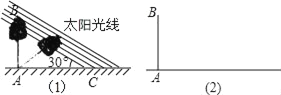
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com