
【题目】雾霾天气给人们的生活带来很大影响,空气质量问题备受人们关注,为了减少雾霾影响,某单位计划为职工购买![]() 、
、![]() 两种型号的防霾口罩.已知每个
两种型号的防霾口罩.已知每个![]() 种型号防霾口罩价格比每个
种型号防霾口罩价格比每个![]() 种型号防霾口罩价格多
种型号防霾口罩价格多![]() 元,花
元,花![]() 元购买
元购买![]() 种型号防霾口罩和花
种型号防霾口罩和花![]() 元购买
元购买![]() 种型号防霾口罩的数量相同.
种型号防霾口罩的数量相同.
(1)求![]() 、
、![]() 两种型号防霾口罩每个价格各多少元?
两种型号防霾口罩每个价格各多少元?
(2)根据单位实际情况,需购买![]() 、
、![]() 两种型号防霾口罩共
两种型号防霾口罩共![]() 个,总费用不高于
个,总费用不高于![]() 万元,求
万元,求![]() 种型号防霾口罩至少要购买多少个?
种型号防霾口罩至少要购买多少个?
【答案】(1)![]() 种型号防霾口罩每个价格为
种型号防霾口罩每个价格为![]() 元,
元,![]() 种型号防霾口罩每个价格为
种型号防霾口罩每个价格为![]() 元;(2)
元;(2)![]() 种型号防霾口罩至少要购买
种型号防霾口罩至少要购买![]() 个
个
【解析】
(1)根据数量=总价÷单价,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)设购买A种型号防霾口罩m个,则购买B种型号防霾口罩(200-m)个,根据总价=单价×数量,即可得出关于m的一元一次不等式,解之取其内的最小正整数即可得出结论.
(1)设A种型号防霾口罩每个价格为x元,则B种型号防霾口罩每个价格为(x+30)元,
根据题意得:![]() ,
,
解得:x=50,
经检验,x=50是原分式方程的解,符合题意,
∴x+30=80.
答:A种型号防霾口罩每个价格为50元,B种型号防霾口罩每个价格为80元.
(2)设购买A种型号防霾口罩m个,则购买B种型号防霾口罩(200-m)个,
根据题意得:50m+80(200-m)≤14000,
解得:![]() .
.
∵m为整数,
∴m≥67.
答:A种型号防霾口罩至少要购买67个.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=x2-2mx-3m
(1)当m=1时,
①抛物线的对称轴为直线______,
②抛物线上一点P到x轴的距离为4,求点P的坐标
③当n≤x≤![]() 时,函数值y的取值范围是-
时,函数值y的取值范围是-![]() ≤y≤2-n,求n的值
≤y≤2-n,求n的值
(2)设抛物线y=x2-2mx-3m在2m-1≤x≤2m+1上最低点的纵坐标为y0,直接写出y0与m之间的函数关系式及m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
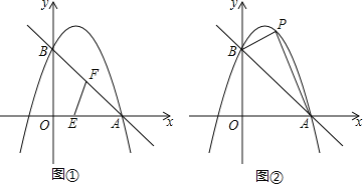
【题目】如图,已知抛物线y=﹣x2+bx+c经过A(3,0),B(0,3)两点.
(1)求此抛物线的解析式和直线AB的解析式;
(2)如图①,动点E从O点出发,沿着OA方 向 以1个单位/秒的速度向终点A匀速运动,同时, 动点F从A点出发,沿着AB方向以![]() 个单位/ 秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
个单位/ 秒的速度向终点B匀速运动,当E,F中任意一点到达终点时另一点也随之停止运动,连接EF,设运动时间为t秒,当t为何值时,△AEF为直角三角形?
(3)如图②,取一根橡皮筋,两端点分别固定在A,B处,用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P与A,B两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时点P的坐标;如果不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.
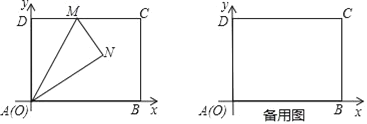
如图,将一个矩形纸片![]() ,放置在平面直角坐标系中,
,放置在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() .
.
(Ⅰ)当![]() 平分
平分![]() 时,求
时,求![]() 的度数和点
的度数和点![]() 的坐标;
的坐标;
(Ⅱ)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)当射线![]() 交线段
交线段![]() 于点
于点![]() 时,求
时,求![]() 的最大值.(直接写出答案)
的最大值.(直接写出答案)
在研究第(Ⅱ)问时,师生有如下对话:
师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题.
小明:我是这样想的,延长![]() 与
与![]() 轴交于
轴交于![]() 点,于是出现了
点,于是出现了![]() .
.
小雨:我和你想的不一样,我过点![]() 作
作![]() 轴的平行线,出现了两个
轴的平行线,出现了两个![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
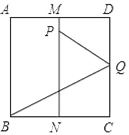
【题目】如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
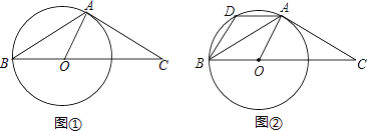
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图①,若⊙O的半径为5,求线段OC的长;
(2)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C (0,3),点P在该抛物线的对称轴上,且纵坐标为2![]() .
.
(1)求抛物线的表达式以及点P的坐标;
(2)当三角形中一个内角α是另一个内角β的两倍时,我们称α为此三角形的“特征角”.
①当D在射线AP上,如果∠DAB为△ABD的特征角,求点D的坐标;
②点E为第一象限内抛物线上一点,点F在x轴上,CE⊥EF,如果∠CEF为△ECF的特征角,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象的一部分,给出下列命题,其中正确的命题是( )(1)
的图象的一部分,给出下列命题,其中正确的命题是( )(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的两根分别-3和1;(4)
的两根分别-3和1;(4)![]() ;
;

A.(1)(2)B.(2)(3)C.(1)(3)D.(1)(3)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com