
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
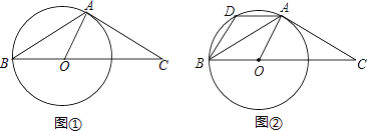
(1)如图①,若⊙O的半径为5,求线段OC的长;
(2)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求![]() 的值.
的值.
【答案】(1)10;(2)![]()
【解析】
(1)求出∠B=∠C=30°,求出∠AOC=60°,求出∠OAC=90°,得出OC=2OA即可.
(2)根据勾股定理求出AC,求出△BOD是等边三角形,求出AC=![]() BD,即可求出答案.
BD,即可求出答案.
(1)∵△ABC中,AB=AC,∠BAC=120°, ∴∠B=∠C=30°,
∵OA=OB,
∴∠BAO=∠B=30°,
∴∠AOC=30°+30°=60°,
∴∠OAC=90°,
∵OA=5,
∴OC=2AO=10.
(2)连接OD,
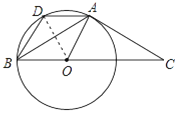
∵∠AOC=60°,AD∥BC,
∴∠DAO=∠AOC=60°,
∵OD=OA,
∴∠ADO=60°,
∴∠DOB=∠ADO=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB=OA,
在Rt△OAC中,OC=2BD,由勾股定理得:AC=![]() BD,
BD,
∴![]() =
=![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某校八年级(1)班语文老师 为了了解学生汉字听写能力情况, 对班上一个组学生的汉字听写成绩 按 A,B,C,D 四个等级进行了 统计,并绘制了如下两幅不完整的统计图:
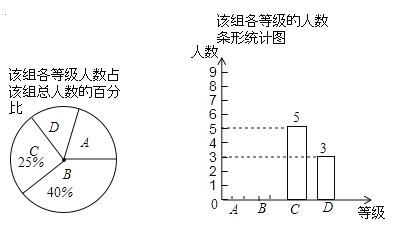
(1)该组学生共有 人;在扇形 统计图中,D 等级所对应的圆心角的 度数是 ;
(2)补全条形统计图;
(3)该组达到 A 等级的同学中只有 1 位男同学,杨老师打算从该组达到 A 等级的同学中随机选出 2 位同学在全班介绍经验,请用列表法或画树状图的方法,求出所选两位同学恰好是 1 位男同学和 1 位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
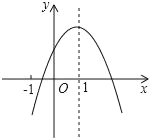
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.
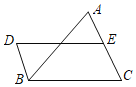
(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)
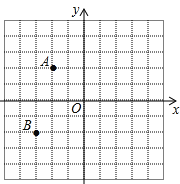
(1)若点D与点A关于y轴对称,则点D的坐标为 .
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为 .
(3)求A,B,C,D组成的四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大
查看答案和解析>>
科目:初中数学 来源: 题型:
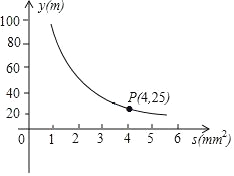
【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)写出y(m)与S(mm2)的函数关系式;
(2)求当面条粗2mm2时,面条的总长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
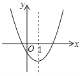
【题目】如图是二次函数![]() 的图象的一部分,对称轴是直线
的图象的一部分,对称轴是直线![]() .
.
①![]() ; ②
; ②![]() ; ③不等式
; ③不等式![]() 的解集是
的解集是![]() ;④若
;④若![]() ,
,![]() 是抛物线上的两点,则
是抛物线上的两点,则![]() . 上述
. 上述![]() 个判断中,正确的是( )
个判断中,正确的是( )
A. ①④ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小山同学结合学习一次函数的经验和自己的思考,按以下方式探究函数![]() 的图象与性质,并尝试解决相关问题.
的图象与性质,并尝试解决相关问题.
请将以下过程补充完整:
(1)判断这个函数的自变量x的取值范围是________________;
(2)补全表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)在平面直角坐标系![]() 中画出函数
中画出函数![]() 的图象:
的图象:
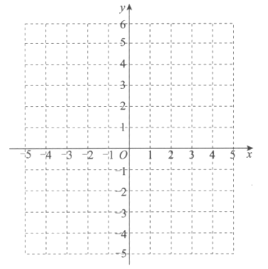
(4)填空:当![]() 时,相应的函数解析式为___(用不含绝对值符合的式子表示);
时,相应的函数解析式为___(用不含绝对值符合的式子表示);
(5)写出直线![]() 与函数
与函数![]() 的图象的交点坐标.
的图象的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com