
【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
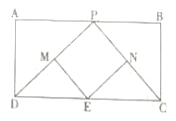
【题目】如图,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形,说明理由.
是菱形,说明理由.
(3)四边形![]() 有可能是矩形吗?若有可能,求出
有可能是矩形吗?若有可能,求出![]() 的长;若不可能,请说明理由.
的长;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题探究】
(![]() )如图①,点
)如图①,点![]() 是正
是正![]() 高
高![]() 上的一定点,请在
上的一定点,请在![]() 上找一点
上找一点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
(![]() )如图②,点
)如图②,点![]() 是边长为
是边长为![]() 的正
的正![]() 高
高![]() 上的一动点,求
上的一动点,求![]() 的最小值.
的最小值.
【问题解决】
(![]() )如图③,
)如图③,![]() 、
、![]() 两地相距
两地相距![]() ,
, ![]() 是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线
是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线![]() 上修一个中转站
上修一个中转站![]() ,再在
,再在![]() 间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由
间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由![]() 到
到![]() 再通过公路由
再通过公路由![]() 到
到![]() 的总运费达到最小值,请确定中转站
的总运费达到最小值,请确定中转站![]() \的位置,并求出
\的位置,并求出![]() 的长.(结果保留根号)
的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
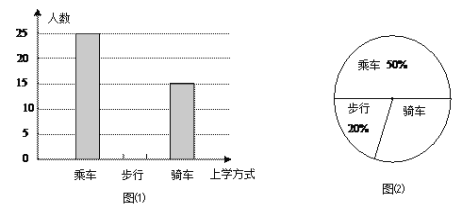
【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)求该班共有多少名学生;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数;
(4)如果全年级共600名同学,请你估算全年级步行上学的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
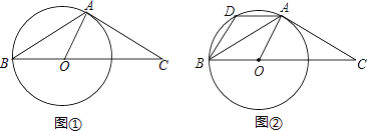
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图①,若⊙O的半径为5,求线段OC的长;
(2)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.

(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
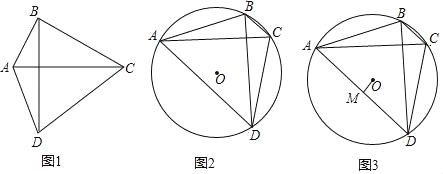
【题目】定义:如果一个四边形的两条对角线相等且相互垂直,则称这个四边形为“等垂四边形”.
如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为“等垂四边形.根据等垂四边形对角线互相垂直的特征可得等垂四边形的一个重要性质:等垂四边形的面积等于两条对角线乘积的一半.根据以上信息解答下列问题:
(1)矩形 “等垂四边形”(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是等垂四边形,若⊙O的半径为6,∠ADC=60°,求四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是等垂四边形,作OM⊥AD于M.请猜想OM与BC的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个.
⑴先从袋中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:若A为必然事件,则m的值为_______,若A为随机事件,则m的取值为______;
⑵若从袋中随机摸出2个球,正好红球、黑球各1个,用列表法与树状图法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC 的∠ABC 的外角平分线 BD 与∠ACB 的外角平分线 CE 交于 P,过 P 作 MN∥AB 交 AC 于M,交 BC 于 N,且 AM=8,BN=5,则 MN=( )
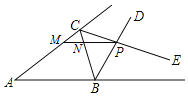
A. 2B. 3C. 4D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com