
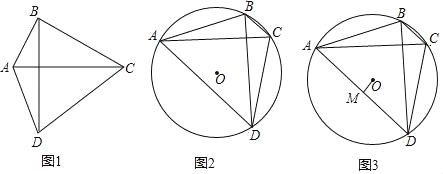
【题目】定义:如果一个四边形的两条对角线相等且相互垂直,则称这个四边形为“等垂四边形”.
如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为“等垂四边形.根据等垂四边形对角线互相垂直的特征可得等垂四边形的一个重要性质:等垂四边形的面积等于两条对角线乘积的一半.根据以上信息解答下列问题:
(1)矩形 “等垂四边形”(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是等垂四边形,若⊙O的半径为6,∠ADC=60°,求四边形ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是等垂四边形,作OM⊥AD于M.请猜想OM与BC的数量关系,并证明你的结论.
【答案】(1)不是;(2)54;(3)OM=![]() BC.
BC.
【解析】
(1)矩形的对角线相等,不一定垂直,所以矩形不一定是等垂四边形.
(2)连接OA,OC,过O作OH⊥AC于H,利用垂径定理求出AC的长即可解决问题;
(3)连接OA,OB,OC,OD,过O作OE⊥BC于E,只要证明△OAM≌△BOE即可解决问题.
解:(1)矩形的对角线相等,不一定垂直,所以矩形不一定是等垂四边形.
故答案为:不是;
(2)连接OA,OC,过O作OH⊥AC于H.
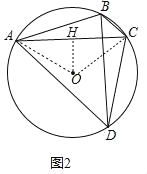
在△AOH中,∠AOH=∠ADC=60,OA=6,
∴AH=3![]() ,
,
∴AC=2AH=6![]() ,
,
∵四边形ABCD是等垂四边形,
∴AC=BD=6![]()
∴S四边形ABCD=![]() ACBD=
ACBD=![]() ×6
×6![]() ×6
×6![]() =54.
=54.
(3)连接OA,OB,OC,OD,过O作OE⊥BC于E,
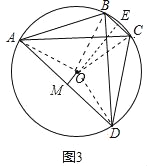
显然∠BOE=∠BAC,∠AOM=∠ABD,
∵BD⊥AC,
∴∠ABD﹢∠BAC=90,
∵∠AOM﹢∠OAM=90,
∴∠OAM=∠BOE,
在△OAM中与△BOE中,
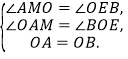
∴△OAM≌△BOE,
∴OM=BE,
∵BE=![]() BC,
BC,
∴OM=![]() BC.
BC.
故答案为:(1)不是;(2)54;(3)OM=![]() BC.
BC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点.
AC,E是AC的中点.
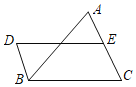
(1)求证:四边形BDEC是平行四边形;
(2)连接AD、BE,△ABC添加一个条件: ,使四边形DBEA是矩形(不需说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大
查看答案和解析>>
科目:初中数学 来源: 题型:
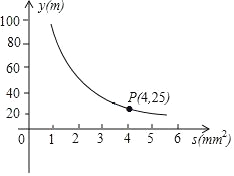
【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)写出y(m)与S(mm2)的函数关系式;
(2)求当面条粗2mm2时,面条的总长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
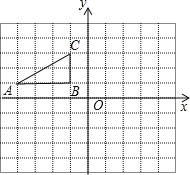
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)先将Rt△ABC向右平移5个单位,再向下平移1个单位后得到Rt△A1B1C1.试在图中画出图形Rt△A1B1C1;
(2)将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出图形Rt△A2B2C2.并计算C1C2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象的一部分,对称轴是直线
的图象的一部分,对称轴是直线![]() .
.
①![]() ; ②
; ②![]() ; ③不等式
; ③不等式![]() 的解集是
的解集是![]() ;④若
;④若![]() ,
,![]() 是抛物线上的两点,则
是抛物线上的两点,则![]() . 上述
. 上述![]() 个判断中,正确的是( )
个判断中,正确的是( )
A. ①④ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
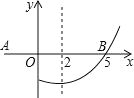
【题目】如图是抛物线 y=ax![]() +bx+c 的一部分,其对称轴为直线 x=2,若其与 x 轴的一个交点为(5,0),则由图象可知,不等式 ax
+bx+c 的一部分,其对称轴为直线 x=2,若其与 x 轴的一个交点为(5,0),则由图象可知,不等式 ax![]() +bx+c<0 的解集是________.
+bx+c<0 的解集是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com