
【题目】注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.
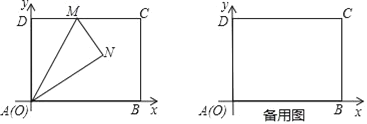
如图,将一个矩形纸片![]() ,放置在平面直角坐标系中,
,放置在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() .
.
(Ⅰ)当![]() 平分
平分![]() 时,求
时,求![]() 的度数和点
的度数和点![]() 的坐标;
的坐标;
(Ⅱ)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)当射线![]() 交线段
交线段![]() 于点
于点![]() 时,求
时,求![]() 的最大值.(直接写出答案)
的最大值.(直接写出答案)
在研究第(Ⅱ)问时,师生有如下对话:
师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题.
小明:我是这样想的,延长![]() 与
与![]() 轴交于
轴交于![]() 点,于是出现了
点,于是出现了![]() .
.
小雨:我和你想的不一样,我过点![]() 作
作![]() 轴的平行线,出现了两个
轴的平行线,出现了两个![]() .
.
【答案】(I)![]() ,
,![]() ;(II)
;(II)![]() ;(III)
;(III)![]() 的最大值为
的最大值为![]() .
.
【解析】
(Ⅰ)由折叠的性质得:△ANM≌△ADM,由角平分线结合得:∠BAM=∠MAN=∠NAB=30°,由特殊角的三角函数可求DM的长,写出M的坐标;
(Ⅱ)如图2,作辅助线,构建直角三角形,设NQ=x,则AQ=MQ=1+x,在Rt△ANQ中,由勾股定理列等式可得关于x的方程:(x+1)2=32+x2,求出x,得出AB是AQ的![]() ,即可得出△NAQ和△NAB的关系,得出结论;
,即可得出△NAQ和△NAB的关系,得出结论;
(III)如图3,过A作AH⊥BF于H,证明△ABH∽△BFC,得![]() ,Rt△AHN中,AH≤AN=3,AB=4,可知:当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图4所示,求此时DF的长即可.
,Rt△AHN中,AH≤AN=3,AB=4,可知:当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,如图4所示,求此时DF的长即可.
(I)如图
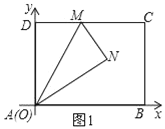
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由折叠得:![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ;
;
(II)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
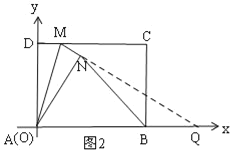
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
由折叠得:![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(III)如图3,过![]() 作
作![]() 于
于![]() ,
,

![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
![]() 当点
当点![]() 、
、![]() 重合(即
重合(即![]() )时,
)时,![]() 最大,
最大,![]() 最小,
最小,![]() 最小,
最小,![]() 最大,此时点
最大,此时点![]() 、
、![]() 重合,
重合,![]() 、
、![]() 、
、![]() 三点共线,如图4所示,
三点共线,如图4所示,
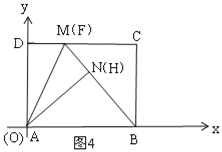
由折叠得:![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]() ,
,
![]() ,
,
由勾股定理得:![]() ,
,
![]() ,
,
![]() 的最大值为
的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有三个小球,上面分别标有数字3、4、5,这些小球除数字不同外其余均相同.
(1)从口袋中随机摸出一个小球,小球上的数字是偶数的概率是______.
(2)从口袋中随机摸出一个小球,记下数字后放回,再随机摸出一个小球,记下数字,请用画树状图(或列表)的方法,求两次摸出的小球上的数字都是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
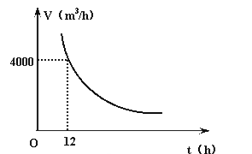
【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_________;
(Ⅱ)解不等式②,得_________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气给人们的生活带来很大影响,空气质量问题备受人们关注,为了减少雾霾影响,某单位计划为职工购买![]() 、
、![]() 两种型号的防霾口罩.已知每个
两种型号的防霾口罩.已知每个![]() 种型号防霾口罩价格比每个
种型号防霾口罩价格比每个![]() 种型号防霾口罩价格多
种型号防霾口罩价格多![]() 元,花
元,花![]() 元购买
元购买![]() 种型号防霾口罩和花
种型号防霾口罩和花![]() 元购买
元购买![]() 种型号防霾口罩的数量相同.
种型号防霾口罩的数量相同.
(1)求![]() 、
、![]() 两种型号防霾口罩每个价格各多少元?
两种型号防霾口罩每个价格各多少元?
(2)根据单位实际情况,需购买![]() 、
、![]() 两种型号防霾口罩共
两种型号防霾口罩共![]() 个,总费用不高于
个,总费用不高于![]() 万元,求
万元,求![]() 种型号防霾口罩至少要购买多少个?
种型号防霾口罩至少要购买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组:![]() ;
;
请结合题意填空,完成本题的解答:
(ⅰ)解不等式(1),得_________;
(ⅱ)解不等式(2),得_________;
(ⅲ)把不等式(1)和(2)的解集在数轴上表示出来:
![]()
(ⅳ)原不等式的解集为:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践:如图△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)作∠BAC的平分线,交BC于点O.
(2)以O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是_____ .(直接写出答案)
(2)若AC=5,BC=12,求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com