
【题目】解不等式组:![]() ;
;
请结合题意填空,完成本题的解答:
(ⅰ)解不等式(1),得_________;
(ⅱ)解不等式(2),得_________;
(ⅲ)把不等式(1)和(2)的解集在数轴上表示出来:
![]()
(ⅳ)原不等式的解集为:__________.
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴分别交于
与x轴分别交于![]() ,
,![]() 两点,与y轴交于点C.
两点,与y轴交于点C.
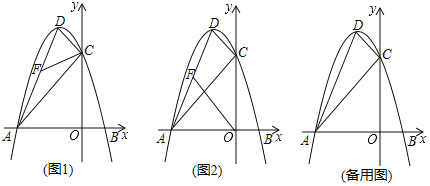
(1)求抛物线的表达式及顶点D的坐标;
(2)点F是线段AD上一个动点.
①如图1,设![]() ,当k为何值时,
,当k为何值时,![]() .
.
②如图2,以A,F,O为顶点的三角形是否与![]() 相似?若相似,求出点F的坐标;若不相似,请说明理由.
相似?若相似,求出点F的坐标;若不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往A县10辆,需要调往B县8辆,已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元;从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元.
(1)设乙仓库调往A县农用车x辆,先填好下表,再写出总运费y关于x的函数关系式;

(2)若要求总运费不超过900元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.
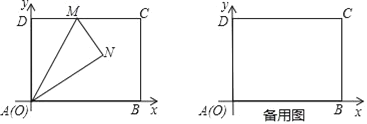
如图,将一个矩形纸片![]() ,放置在平面直角坐标系中,
,放置在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() .
.
(Ⅰ)当![]() 平分
平分![]() 时,求
时,求![]() 的度数和点
的度数和点![]() 的坐标;
的坐标;
(Ⅱ)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)当射线![]() 交线段
交线段![]() 于点
于点![]() 时,求
时,求![]() 的最大值.(直接写出答案)
的最大值.(直接写出答案)
在研究第(Ⅱ)问时,师生有如下对话:
师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题.
小明:我是这样想的,延长![]() 与
与![]() 轴交于
轴交于![]() 点,于是出现了
点,于是出现了![]() .
.
小雨:我和你想的不一样,我过点![]() 作
作![]() 轴的平行线,出现了两个
轴的平行线,出现了两个![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
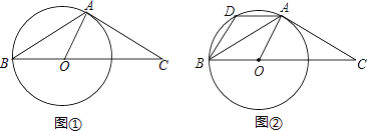
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图①,若⊙O的半径为5,求线段OC的长;
(2)如图②,过点A作AD∥BC交⊙O于点D,连接BD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() .对角线
.对角线![]() 相交于点
相交于点![]() ,反比例函数
,反比例函数![]() 的图像经过点
的图像经过点![]() ,分别与
,分别与![]() 交于点
交于点![]() .
.
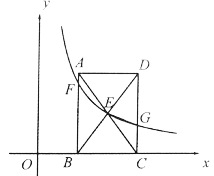
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,AB=AC,边BC长为6,高AD长为4,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,则正方形PQMN的边长为( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com