
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=50°,AC=6,求图中阴影部分的面积.

【答案】(1)直线DE与⊙O相切,见解析;(2)6-![]() π
π
【解析】
(1)连接OE、OD,根据切线的性质得到∠OAC=90°,根据三角形中位线定理得到OE∥BC,证明△AOE≌△DOE,根据全等三角形的性质、切线的判定定理证明;
(2)根据扇形的面积公式计算即可.
解:(1)直线DE与⊙O相切,
理由如下:连接OE、OD,如图,
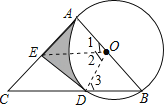
∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵点E是AC的中点,O点为AB的中点,
∴OE∥BC,
∴∠1=∠B,∠2=∠3,
∵OB=OD,
∴∠B=∠3,
∴∠1=∠2,
在△AOE和△DOE中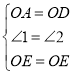 ,
,
∴△AOE≌△DOE(SAS)
∴∠ODE=∠OAE=90°,
∴DE⊥OD,
∵OD为⊙O的半径,
∴DE为⊙O的切线;
(2)∵DE、AE是⊙O的切线,
∴DE=AE,
∵点E是AC的中点,
∴AE=![]() AC=3,
AC=3,
∠AOD=2∠B=2×50°=100°,
∴图中阴影部分的面积=2×![]() ×2×3﹣
×2×3﹣![]() =6-
=6-![]() π.
π.


科目:初中数学 来源: 题型:
【题目】注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.
如图,将一个矩形纸片![]() ,放置在平面直角坐标系中,
,放置在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() .
.
(Ⅰ)当![]() 平分
平分![]() 时,求
时,求![]() 的度数和点
的度数和点![]() 的坐标;
的坐标;
(Ⅱ)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(Ⅲ)当射线![]() 交线段
交线段![]() 于点
于点![]() 时,求
时,求![]() 的最大值.(直接写出答案)
的最大值.(直接写出答案)
在研究第(Ⅱ)问时,师生有如下对话:
师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题.
小明:我是这样想的,延长![]() 与
与![]() 轴交于
轴交于![]() 点,于是出现了
点,于是出现了![]() .
.
小雨:我和你想的不一样,我过点![]() 作
作![]() 轴的平行线,出现了两个
轴的平行线,出现了两个![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() .对角线
.对角线![]() 相交于点
相交于点![]() ,反比例函数
,反比例函数![]() 的图像经过点
的图像经过点![]() ,分别与
,分别与![]() 交于点
交于点![]() .
.
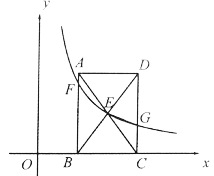
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(![]() ,0),有下列结论:
,0),有下列结论:
①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-bm≥(am-b);其中所有正确的结论有( )个.
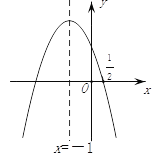
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
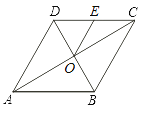
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象的一部分,给出下列命题,其中正确的命题是( )(1)
的图象的一部分,给出下列命题,其中正确的命题是( )(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的两根分别-3和1;(4)
的两根分别-3和1;(4)![]() ;
;

A.(1)(2)B.(2)(3)C.(1)(3)D.(1)(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,AB=AC,边BC长为6,高AD长为4,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,则正方形PQMN的边长为( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD顶点B(﹣1,﹣1),C在x轴正半轴上,A在第二象限双曲线y=﹣![]() 上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
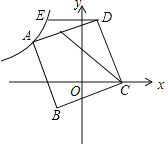
A.3B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
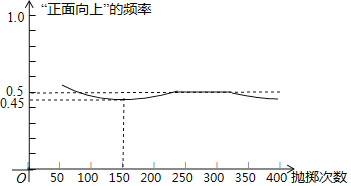
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com