Question

5．下面的图形是用小棋子摆成的“小雨伞”，

根据规律得出第n个“小雨伞”需要棋子的个数用代数式5n+1来表示．

Answer 1

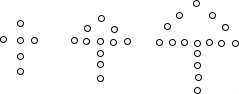
分析 由题意可知：第1个“小雨伞”需要棋子的个数是1+2+1+2，第2个“小雨伞”需要棋子的个数是1+2+4+1+3，第3个“小雨伞”需要棋子的个数是1+2×2+6+1+4，…由此得出第n个“小雨伞”需要棋子的个数是1+2（n-1）+2n+1+（n+1），由此得出答案即可．

解答 解：∵第1个“小雨伞”需要棋子的个数是1+2+1+2=6，
第2个“小雨伞”需要棋子的个数是1+2+4+1+3=11，
第3个“小雨伞”需要棋子的个数是1+2×2+6+1+4=16，
…
∴第n个“小雨伞”需要棋子的个数是1+2（n-1）+2n+1+（n+1）=5n+1．
故答案为：5n+1．

点评 此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．