
【题目】如图,抛物线经过点A(﹣1,0)和B(0,2 ![]() ),对称轴为x=
),对称轴为x= ![]() .
.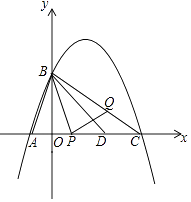
(1)求抛物线的解析式;
(2)抛物线与x轴交于另一个交点为C,点D在线段AC上,已知AD=AB,若动点P从A出发沿线段AC以每秒1个单位长度的度数匀速运动,同时另一动点Q以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻,使线段PQ被直线BD垂直平分?若存在,求出点Q的运动速度;若不存在,请说明理由.
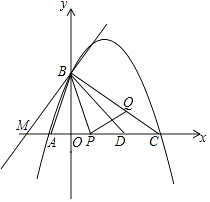
(3)在(2)的前提下,过点B的直线l与x轴的负半轴交于点M,是否存在点M,使以A,B,M为顶点的三角形与△PBC相似?如果存在,请直接写出M的坐标;若不存在,请说明理由.
【答案】
(1)
解:设抛物线的解析式为y=a(x﹣ ![]() )2+k,(a≠),
)2+k,(a≠),
把点A(﹣1,0)和B(0,2 ![]() )代入得到
)代入得到 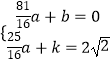 ,
,
解得 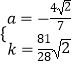 ,
,
∴y=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴y=﹣ ![]() x2+
x2+ ![]() x+2
x+2 ![]()
(2)
解:令y=0得到﹣ ![]() x2+
x2+ ![]() x+2
x+2 ![]() =0,解得x=
=0,解得x= ![]() 或﹣1,
或﹣1,
∴C( ![]() ,0),A(﹣1,0),AB=
,0),A(﹣1,0),AB= ![]() =3,
=3,
∵AD=AB,
∴AD=3,
∴D(2,0),
∵PB被BD垂直平分,
∴BP=BQ,
∴∠DBP=∠DBQ,
∴ ![]() (角平分线的性质定理,可以用面积法证明),
(角平分线的性质定理,可以用面积法证明),
∴ ![]() =
= ![]() ,
,
∴t=2或 ![]() ,
,
∵t<3,
∴t=2,
∴BP=3,BQ=3,
∴VQ= ![]()
(3)
解:存在.理由如下:
由题意P(1,0),PB=3,PC= ![]() ,
,
∵BA=BP=2,
∴∠BAP=∠BPA,
∴∠BPC=∠BAM,
①当 ![]() ,△MAB∽△BPC,
,△MAB∽△BPC,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() ,OM=OA+AM=
,OM=OA+AM= ![]()
∴M(﹣ ![]() ,0).
,0).
②当 ![]() 时,△MAB∽CPB,
时,△MAB∽CPB,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() ,OM=AM+OA=
,OM=AM+OA= ![]() ,
,
∴M(﹣ ![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x﹣ ![]() )2+k,(a≠),把点A(﹣1,0)和B(0,2
)2+k,(a≠),把点A(﹣1,0)和B(0,2 ![]() )代入,解方程组即可解决问题.(2)首先求出A、C坐标,由∠DBP=∠DBQ,可得
)代入,解方程组即可解决问题.(2)首先求出A、C坐标,由∠DBP=∠DBQ,可得 ![]() (角平分线的性质定理,可以用面积法证明),即
(角平分线的性质定理,可以用面积法证明),即 ![]() =
= ![]() ,解方程即可解决问题.(3)存在.理由如下:首先证明∠BPC=∠BAM,分两种情形讨论①当
,解方程即可解决问题.(3)存在.理由如下:首先证明∠BPC=∠BAM,分两种情形讨论①当 ![]() ,△MAB∽△BPC,列出方程解方程即可.②当
,△MAB∽△BPC,列出方程解方程即可.②当 ![]() 时,△MAB∽CPB,列出方程解方程即可.
时,△MAB∽CPB,列出方程解方程即可.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为参加全区的“我爱古诗词”知识竞赛,王晓所在学校组织了一次古诗词知识测试![]() 王晓从全体学生中随机抽取部分同学的分数
王晓从全体学生中随机抽取部分同学的分数![]() 得分取正整数,满分为100分
得分取正整数,满分为100分![]() 进行统计
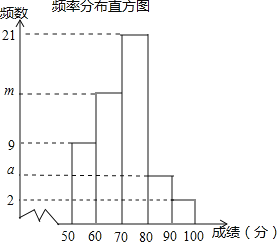
进行统计![]() 以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图
以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图![]() 请根据以上频率分布表和布直方图,回答下列问题:
请根据以上频率分布表和布直方图,回答下列问题:
组别 | 分组 | 频数 | 频率 |
1 |
| 9 |
|
2 |
| m | b |
3 |
| 21 |
|
4 |
| a |
|
5 |
| 2 | n |
(1)分别求出a、b、m、n的值;![]() 写出计算过程
写出计算过程![]()
(2)老师说:“王晓的测试成绩是被抽取的同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)得分在![]() 的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?
的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、![]() 分别是锐角三角形ABC和锐角三角形
分别是锐角三角形ABC和锐角三角形![]() 中BC、
中BC、![]() 边上的高,且
边上的高,且![]() 、
、![]() .若使△ABC≌△
.若使△ABC≌△![]() ,请你补充条件_________.(填写一个你认为适当的条件即可)
,请你补充条件_________.(填写一个你认为适当的条件即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 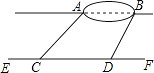
查看答案和解析>>
科目:初中数学 来源: 题型:
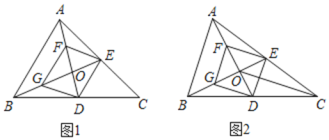
【题目】如图,在![]() 中,点D,E分别是边BC,AC的中点,AD与BE相交于点
中,点D,E分别是边BC,AC的中点,AD与BE相交于点![]() 点F,G分别是线段AO,
点F,G分别是线段AO,
BO的中点.
![]() 求证:四边形DEFG是平行四边形;
求证:四边形DEFG是平行四边形;
![]() 如图2,连接CO,若
如图2,连接CO,若![]() ,求证:四边形DEFG是菱形;
,求证:四边形DEFG是菱形;
![]() 在
在![]() 的前提下,当
的前提下,当![]() 满足什么条件时,四边形DEFG能成为正方形?
满足什么条件时,四边形DEFG能成为正方形?![]() 直接回答即可,不必证明
直接回答即可,不必证明![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则Sn的值为 . (用含n的代数式表示,n为正整数) 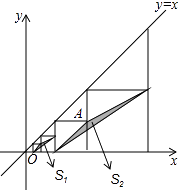
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初中三年级270名师生计划集体外出一日游,乘车往返,经与客运公司联系,他们有座位数不同的中巴车和大客车两种车型可供选择,每辆大客车比中巴车多15个座位,学校根据中巴车和大客车的座位数计算后得知,如果租用中巴车若干辆,师生刚好坐满全部座位;如果租用大客车,不仅少用一辆,而且师生坐完后还多30个座位.
(1)求中巴车和大客车各有多少个座位?
(2)客运公司为学校这次活动提供的报价是:租用中巴车每辆往返费用350元,租用大客车每辆往返费用400元,学校在研究租车方案时发现,同时租用两种车,其中大客车比中巴车多租一辆,所需租车费比单独租用一种车型都要便宜,按这种方案需要中巴车和大客车各多少辆?租车费比单独租用中巴车或大客车各少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO. 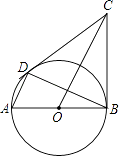
(1)求证:△ADB∽△OBC;
(2)连结CD,试说明CD是⊙O的切线;
(3)若AB=2, ![]() ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com