
【题目】如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD. 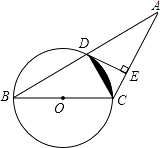
(1)求证:DE为⊙O的切线;
(2)若AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】
(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠ODB.又∵∠A=∠B=30°,
∴∠A=∠ODB,
∴DO∥AC,
∵DE⊥AC,
∴OD⊥DE.
∴DE 为⊙O 的切线
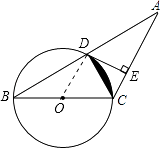
(2)解:∵BC 为直径,
∴∠BDC=90°.
根据等腰三角形的三线合一性质得到CD是AB的中线,
∴BD= ![]() AB=2
AB=2 ![]() ,
,
在直角三角形BDC中,cosB═ ![]() ,即
,即 ![]() =
= ![]() ,
,
解得BC=4,
S阴影=S扇形OCD﹣S△OCD= ![]() ﹣
﹣ ![]() ×
× ![]() =
= ![]() ﹣
﹣ ![]()
【解析】(1)首先连接OD,根据等边对等角得出∠B=∠ODB,又由等腰三角形ABC的底角为30°,可得∠A=∠ODB,即可证得OD∥AC,继而可证得结论;(2)由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD= ![]() AB=2
AB=2 ![]() ,通过解余弦函数求得BC,从而得出圆的半径,进而根据S阴影=S扇形OCD﹣S△OCD即可求得.
,通过解余弦函数求得BC,从而得出圆的半径,进而根据S阴影=S扇形OCD﹣S△OCD即可求得.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线),还要掌握扇形面积计算公式(在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2))的相关知识才是答题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) 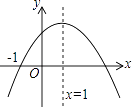
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列给出四个命题:
①直角三角形的两边是方程y2-7y+12=0的两根,则它的第三边是5;
②若一元二次方程ax2+bx+c=0(a≠0)的系数a,c异号,则该方程有两个不相等的实数根;
③若一元二次方程(m-2)x2+x+m2-4=0有一个根为0,那么m=±2;
④已知一元二次方程ax2+bx+c=0(a≠0)中a,b,c满足a-b+c=0,4a+2b+c=0则方程的两根为x1=-1,x2=2;其中真命题的是__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一出租车一天下午以鼓楼为出发地在东西方向运营,向东走为正,向西走为负,行车里程(单位:㎞)依先后次序记录如下:+9,-3,-5,+4,-8,+6,-3,-6,-4,+10.
⑴将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
⑵若每千米的价格为2.4元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
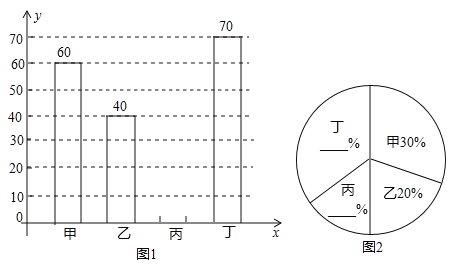
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树的棵树和所占百分比情况进行了调查,将收集的数据整理并绘制成图1和图2两幅不完整的统计图,请根据图中的信息,完成下列问题:
(1)这四个班共植树 棵;
(2)请补全两幅统计图;
(3)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树大约有多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点. 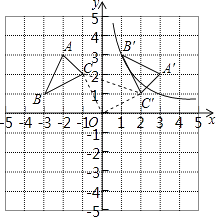
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:13=1=![]() ;13+23=9=
;13+23=9=![]() ;13+23+33=36=
;13+23+33=36=![]() ;13+23+33+43=100=
;13+23+33+43=100=![]() ,
,
回答下面的问题:
(1)13+23+33+43+…+103=_____(写出算式即可);
(2)计算13+23+33+…+993+1003的值;
(3)计算:113+123+…+993+1003的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com