
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】某校5月组织了学生参加“学习强国”知识竞赛,从中抽取了部分学生成绩(满分为100分)进行统计,绘制如下不完整的频数直方图,若将频数直方图划分的五组从左至右依次记为A、B、C、D、E,绘制如下扇形统计图,请你根据图形提供的信息,解答下列问题:
(1)频数分布直方图中,A组的频数a= ,并补全频数直方图;
(2)扇形统计图中,D部分所占的圆心角n= 度;
(3)若成绩在80分以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,BE∥AC,AE∥OB.函数![]() (k>0,x>0)的图象经过点E.若点A、C的坐标分别为(3,0)、(0,2),则k的值为( )
(k>0,x>0)的图象经过点E.若点A、C的坐标分别为(3,0)、(0,2),则k的值为( )
A. 3 B. 4 C. 4.5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国很多地区持续出现雾霾天气.某社区为了调查本社区居民对雾霾天气主要成因的认识情况,随机对该社区部分居民进行了问卷调查,要求居民从五个主要成因中只选择其中的一项,被调查居民都按要求填写了问卷.社区对调查结果进行了整理,绘制了如下不完整的统计图表.被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数(人数) |
A大气气压低,空气不流动 | m |
B地面灰尘大,空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题:

(1)填空:m=________,n=________,扇形统计图中C选项所占的百分比为________.
(2)若该社区居民约有6 000人,请估计其中会选择D选项的居民人数.
(3)对于“雾霾”这个环境问题,请你用简短的语言发出倡议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,
厘米,![]() 、
、![]() 是
是![]() 边上的两个动点,其中点
边上的两个动点,其中点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,速度为1厘米/秒,点
方向运动,速度为1厘米/秒,点![]() 从点
从点![]() 开始沿
开始沿![]() 方向运动,速度为2厘米/秒,若它们同时出发,设出发的时间为
方向运动,速度为2厘米/秒,若它们同时出发,设出发的时间为![]() 秒.
秒.

(1)求出发2秒后,![]() 的长.
的长.
(2)点![]() 在
在![]() 边上运动时,当
边上运动时,当![]() 成为等腰三角形时,求点
成为等腰三角形时,求点![]() 的运动时间.
的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装商场购进一批T恤,每件进价40元,出于营销考虑,要求每件售价不得低于40元且不得高于60元,在销售过程中发现该T恤每周的销售量![]() (件)与每件售价
(件)与每件售价![]() (元)之间满足一次函数关系:当销售单价为44元时,销量是72件,当销售单价为48元时,销售量为64件.
(元)之间满足一次函数关系:当销售单价为44元时,销量是72件,当销售单价为48元时,销售量为64件.
(1)请直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当商场每周销售这种T恤获得350元的利润时,每件的销售单价是多少元?
(3) 设该商场每周销售这种T恤所获得的利润为![]() 元,将该T恤销售单价定为多少元时,才能使商场销售该T恤所获利润最大?最大利润是多少?
元,将该T恤销售单价定为多少元时,才能使商场销售该T恤所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
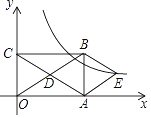
【题目】 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(![]() ,0)、(0,4),抛物线
,0)、(0,4),抛物线![]() 经过B点,且顶点在直线
经过B点,且顶点在直线![]() 上.
上.

【1】(1)求抛物线对应的函数关系式;
【2】(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
【3】(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com