
【题目】如图1,正方形ABCD的一边AB在直尺一边所在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E.

(1)如图1,线段AB与OE之间的数量关系为 .(请直接填结论)
(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转θ(0<θ<90°),过点 B作BF⊥MN于点F.
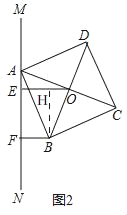
①如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.
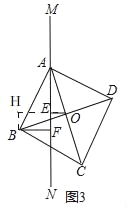
②如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
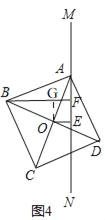
③当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为 .(请直接填结论)
【答案】(1)AB=2OE;(2)①AF+BF=2OE,证明见解析;②AF﹣BF=2OE 证明见解析;③BF﹣AF=2OE,
【解析】试题分析:(1)利用直角三角形斜边的中线等于斜边的一半即可得出结论;
(2)①过点B作BH⊥OE于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;
②过点B作BH⊥OE交OE的延长线于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBH,然后利用“角角边”证明△AOE和△OBH全等,根据全等三角形对应边相等可得OH=AE,OE=BH,再根据AF-EF=AE,整理即可得证;
③同②的方法可证.
试题解析:(1)∵AC,BD是正方形的对角线,
∴OA=OC=OB,∠BAD=∠ABC=90°,
∵OE⊥AB,
∴OE=![]() AB,
AB,
∴AB=2OE,
(2)①AF+BF=2OE
证明:如图2,过点B作BH⊥OE于点H
∴∠BHE=∠BHO=90°
∵OE⊥MN,BF⊥MN
∴∠BFE=∠OEF=90°
∴四边形EFBH为矩形
∴BF=EH,EF=BH
∵四边形ABCD为正方形
∴OA=OB,∠AOB=90°
∴∠AOE+∠HOB=∠OBH+∠HOB=90°
∴∠AOE=∠OBH
∴△AEO≌△OHB(AAS)
∴AE=OH,OE=BH
∴AF+BF=AE+EF+BF=OH+BH+EH=OE+OE=2OE.
②AF﹣BF=2OE
证明:如图3,延长OE,过点B作BH⊥OE于点H
∴∠EHB=90°
∵OE⊥MN,BF⊥MN
∴∠AEO=∠HEF=∠BFE=90°
∴四边形HBFE为矩形
∴BF=HE,EF=BH
∵四边形ABCD是正方形
∴OA=OB,∠AOB=90°
∴∠AOE+∠BOH=∠OBH+∠BOH
∴∠AOE=∠OBH
∴△AOE≌△OBH(AAS)
∴AE=OH,OE=BH,
∴AF﹣BF
=AE+EF﹣HE=OH﹣HE+OE=OE+OE=2OE
③BF﹣AF=2OE,
如图4,作OG⊥BF于G,则四边形EFGO是矩形,
∴EF=GO,GF=EO,∠GOE=90°,
∴∠AOE+∠AOG=90°.
在正方形ABCD中,OA=OB,∠AOB=90°,
∴∠AOG+∠BOG=90°,
∴∠AOE=∠BOG.
∵OG⊥BF,OE⊥AE,
∴∠AEO=∠BGO=90°.
∴△AOE≌△BOG(AAS),
∴OE=OG,AE=BG,
∵AE﹣EF=AF,EF=OG=OE,AE=BG=AF+EF=OE+AF,
∴BF﹣AF=BG+GF﹣(AE﹣EF)=AE+OE﹣AE+EF=OE+OE=2OE,
∴BF﹣AF=2OE.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
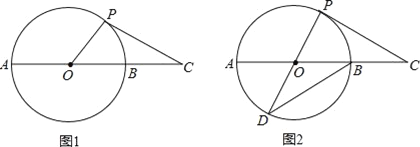
【题目】如图1,延长⊙O的直径AB至点C,使得BC=![]() AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 的边
的边![]() 平行于
平行于![]() 轴,
轴,![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第四象限,点
在第四象限,点![]() 是
是![]() 边上的一个动点.
边上的一个动点.

(1)若点![]() 在边
在边![]() 上,
上,![]() 求点
求点![]() 的坐标;
的坐标;
(2)若点![]() 在边
在边![]() 或
或![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点如图2,过点
轴的交点如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 过点
过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 它们相交于点
它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
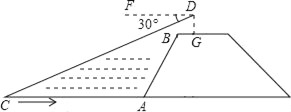
【题目】如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时测得小船C的俯角是∠FDC=30°.若小华的眼睛与地面的距离是![]() 米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
米,BG=1.5米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=10米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长是多少?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
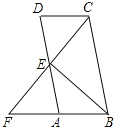
【题目】如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=100°,求∠ABE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化校园,某学校将要购进A、B两个品种的树苗,已知一株A品种树苗比一株B品种树苗多20元,若买一株A品种树苗和2株B品种树苗共需110元.
(1)问A、B两种树苗每株分别是多少元?
(2)学校若花费不超过4000元购入A、B两种树苗,已知A品种树苗数量是B品种树苗数量的一半,问此次至多购买B品种树苗多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
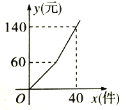
【题目】某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每天薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的( )
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产45件.
D.人乙一天生产40(件),则他获得薪金140元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com